ウエハースケール計算エンジンWSE-2においてSimulated-Annealingを実装しました

ウエハースケール計算エンジンにSimulated annealingを実装しました。コーディング方法と解説をしています。また、そのソースコードを公開しています。
このブログは、株式会社フィックスターズのエンジニアが、あらゆるテーマについて自由に書いているブログです。

ウエハースケール計算エンジンにSimulated annealingを実装しました。コーディング方法と解説をしています。また、そのソースコードを公開しています。

Intel Developer Cloudを使用すると、Intel製CPUの評価を簡単に行うことができます。
物体認識モデルであるYOLOv8の評価を題材に、性能評価を行う方法を紹介します。

「安全に」プログラムを実行できる TEE は、DRM など様々な用途で利用されています。
TEE は実現方式・実装が複数存在しますが、本記事では ARM TrustZone を用いる商用 TEE “Kinibi” の基本動作を紹介します。

モンゴメリ乗算のプログラムを Intel AVX-512IFMA52 命令セットを用いて実装し、他の実装と比較しつつ、パフォーマンス分析を行い、効果を確かめます。結果的には AVX-512IFMA52 命令セットを用いない SIMD 実装に対して 85% の高速化を達成しました。

生産計画未経験者がFixstars Amplify Scheduling Engineを使って、半導体製造工程における仮想のテスト計画のスケジューリング最適化を試みました。
Fixstars Amplify Scheduling Engineは、Fixstars Amplify SDKから利用することができます。以下はSDKを用いたプログラム例です。

SfMなどで用いられる、2値特徴記述アルゴリズムであるHashSIFTの概要とCUDAによる高速化手法について紹介します。

今回はVisual SLAMやSfM(Structure from Motion)で行われる局所特徴量計算について、CUDAによる高速化に取り組んだ話を紹介します。
また、そのソースコードをcuda-efficient-featuresという名前でGitHubに公開しています。
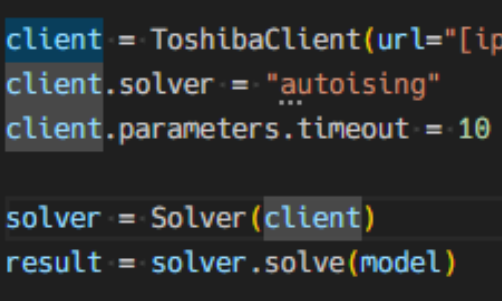
2020年記事「シミュレーテッド分岐マシン(SBM)で巡回セールスマン問題を解く」 を題材にして、アップグレードした量子インスパイアード最適化ソリューション「Toshiba SQBM+」の新機能である、AUTOISINGソルバについてご紹介します。
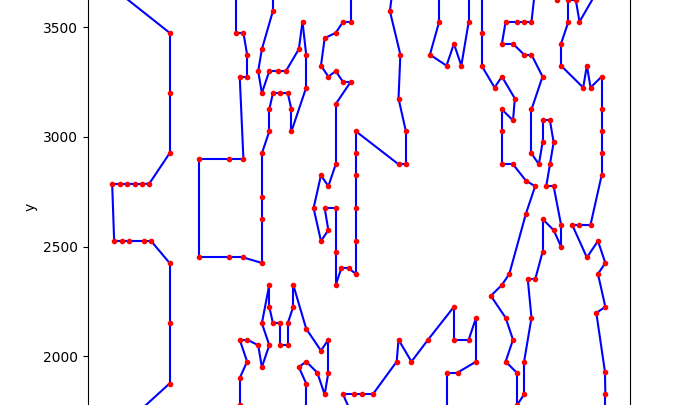
東芝デジタルソリューションズ提供のシミュレーテッド分岐マシン(SBM)は、それを核とする量子インスパイアード最適化ソリューション「Toshiba SQBM+」と名称を改めて現在提供されています。
これから2回に分けて、この新しい SQBM+の機能をご紹介します。

フィックスターズでは、耐量子の公開鍵暗号である CRYSTALS-KYBER の高速な実装に取り組んでいます。今回は導入編として、CRYSTALS-KYBERの数理的な背景と公開鍵暗号の安全性の考え方について簡単に説明します。

teb_local_planner のアルゴリズムの概要を理解し、パラメータ調整ができるようになることを目的として解説します。

2022年12月に開催された Kaggle コンテスト「 Santa 2022 – The Christmas Card Conundrum 」の概要と解法について紹介します。

単一ソースで計算をGPU上で実行できる規格SYCLの実装のうち、活発に開発されているものを実際にインストールし、同じ計算コードで得られる性能を比較しました。
2022年7月から10月にかけて開催されたKaggleコンペティション DFL – Bundesliga Data Shootout に弊社エンジニア3名のチームで参加し、530チーム中6位の成績を収めました。
この結果弊社チームに金メダルが与えられ、2名がKaggle Competitions Masterの称号を獲得しました。
本投稿ではコンペの概要と解法について紹介します。

Livox社から新たに3D LiDAR「Mid-360」が発売されました。この記事では、Mid-360のROS1/ROS2での動かし方について紹介します。

rosbag2_storage_mcapパッケージが追加され、rosbag2のストレージとしてMCAPが選択できるようになりました。この記事ではrosbag2_storage_mcapの使い方を紹介します。

この記事はC++ Advent Calendar 2022の9日目の記事です。 皆さまこんにちは。今日もソフトウェア高速化してますか? 私も相変わらず色々と高速化している日々ですが、最近、私が書いたループ展開のコードを見 […]
はじめに こんにちは、Fixstars Autonomous Technologiesの鈴木です。 自動運転やロボットなどの分野でSLAMと呼ばれる技術があります。SLAMとは「Simultaneous Localiza […]
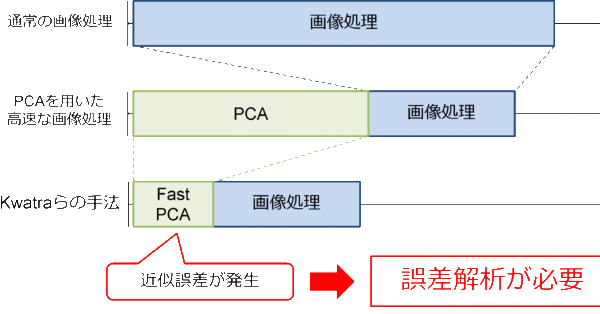
来る12月2日、ビジョン技術の実利用ワークショップ(ViEW2021)にて、『画像の次元削減のための高速共分散行列計算における近似誤差解析手法の提案』というタイトルで論文発表を行います。 日時2021年12月2日(木)1 […]
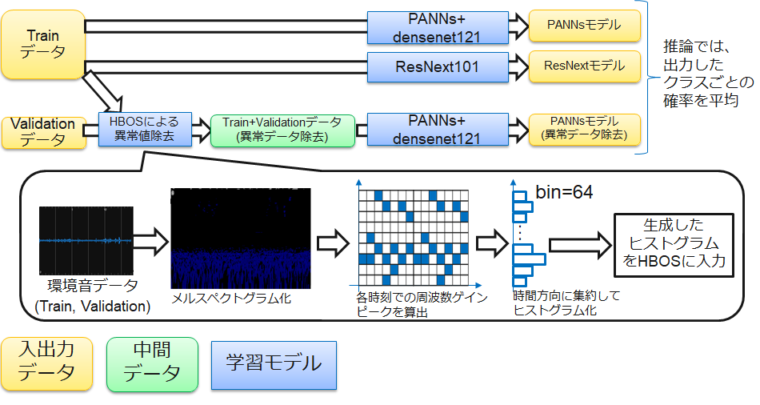
概要 Fixstars Autonomous Technologiesの重岡です。2021/4-5月に実施されたKaggleのコンペティション(BirdCLEF2021)に参加して、銀メダル(816チーム中37 […]
コンピュータビジョンセミナーvol.2 開催のお知らせ - ニュース一覧 - 株式会社フィックスターズ in Realizing Self-Driving Cars with General-Purpose Processors 日本語版
[…] バージョンアップに伴い、オンラインセミナーを開催します。 本セミナーでは、�...
【Docker】NVIDIA SDK Managerでエラー無く環境構築する【Jetson】 | マサキノート in NVIDIA SDK Manager on Dockerで快適なJetsonライフ
[…] 参考:https://proc-cpuinfo.fixstars.com/2019/06/nvidia-sdk-manager-on-docker/ […]...
Windowsカーネルドライバを自作してWinDbgで解析してみる① - かえるのほんだな in Windowsデバイスドライバの基本動作を確認する (1)
[…] 参考:Windowsデバイスドライバの基本動作を確認する (1) - Fixstars Tech Blog /proc/cpuinfo ...
2021年版G検定チートシート | エビワークス in ニューラルネットの共通フォーマット対決! NNEF vs ONNX
[…] ONNX(オニキス):Open Neural Network Exchange formatフレームワーク間のモデル変換ツー�...
YOSHIFUJI Naoki in CUDAデバイスメモリもスマートポインタで管理したい
ありがとうございます。別に型にこだわる必要がないので、ユニバーサル参照を受けるよ...