Segment Tree を少し速くする

Segment Treeと呼ばれるデータ構造があります。
プログラミングコンテストでも解法の一部として使われることが多いため、よくコンテストに参加するような人だとコピペで使えるように準備しているということも多いのではないかと思います。
このデータ構造を使うと、1次元の数列に対する以下の操作が $O(\log n)$ の時間計算量で可能となります。

• query(l, r): $a_{l}\ \textrm{op}\ a_{l+1}\ \textrm{op}\ \cdots\ \textrm{op}\ a_{r-2}\ \textrm{op}\ a_{r-1}$ を求める
• update(i, x): $a_{i}$ に $x$ を代入する

たとえば、最初に数列 $a = [ 0, 1, 2, 3 ]$ があり、$x\ \textrm{op}\ y$ が $\min(x, y)$ であるときのクエリ処理結果の例は以下のようになります。

• query(0, 4) => min(0, 1, 2, 3) => 0
• update(1, 8)
• query(1, 3) => min(8, 2) => 2
• query(0, 3) => min(0, 8, 2) => 0
• update(0, 3)
• query(0, 4) => min(3, 8, 2, 3) => 2

どのようにクエリ処理を実現しているかというと、以下の図のように$2^k$個の連続した要素をまとめた結果を事前に求めておくことにより、任意の長さの区間クエリを高々 $O(\log n)$ 個の事前計算済みの区間の結果から求めています。

この木の各頂点の値を、根から近い順にならべて1次元配列として持つという方法が（プログラミングコンテストでは）よく用いられているようです。
このように並べてやると、$k$番目の要素の子は$2k+1$番目の要素と$2k+2$番目の要素といったように、明示的に辺の情報を持たずに完全二分木を表現することができます。

Top-downとBottom-up

クエリ処理の際、区間をちょうどカバーするようなノードの集合を得る必要があります。

この部分の処理は、$k$番目の要素が対応する区間を引数に持ち、その区間が $[l, r)$ に完全に含まれるようならその要素の値を返し、そうでなければ区間を2分割し、それぞれについてまた $[l, r)$ に含まれるかどうかを判定して……といったような関数を再帰的に呼んでいくようなコードをよく見ます。（参考: PEG Wiki, プログラミングコンテストチャレンジブック）

# tree: 上述の完全二分木をあらわすデータ
recur(k, a, b, l, r):
  # [a, b): tree中のk番目の要素に対応する区間
  # [l, r): クエリの引数となる区間
  if [a, b) が [l, r) に完全に含まれる:
    return tree[k]
  if [a, b) と [l, r) に共通の区間が存在しない:
    return opの単位元
  c = (a + b) / 2
  return recur(k * 2 + 1, a, c, l, r) op recur(k * 2 + 2, c, b, l, r)

この方法は木を上からたどっていくようなイメージになるのですが、再帰があったり区間の計算がやや面倒だったりと、データの並びなどを変えずとも改善する余地がありそうに見えます。

木をたどるとき、根のほうからではなく葉のほうからたどることを考えてみます。
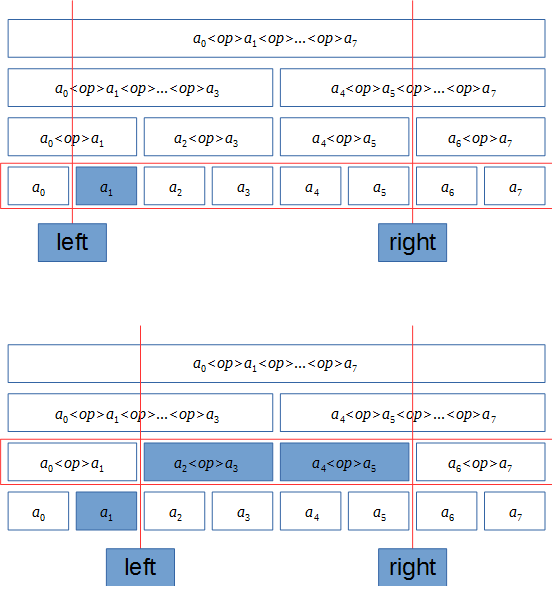
もともとの数列における1つの連続した要素に対応する部分列を考えると、$l$が奇数のときにはその層で$l$番目の要素に対応する値をくわえる必要があります。（それより上の層では$l-1$番目の要素を加えずに$l$番目の要素を加えることができないため。）同様に、$r$が奇数の時には$r-1$番目の要素を加える必要があります。
要素を加えたらその分だけ$l$, $r$をずらして、次の層についてまた同様に処理を行い、それを $l = r$ となるまで繰り返します。

以下に、$n = 8, l = 1, r = 6$ の場合のイメージを示します。

こうすることでも、区間クエリに回答するために必要な最小の要素の集合を得ることができます。
この方法だと、単純な繰り返しで済んだり区間にまつわる処理が簡単になるため、多少の高速化が期待できます。

実装

C++での各クエリ処理の実装と、性能評価のためのコードは、以下のようになりました。

#include <iostream>
#include <vector>
#include <algorithm>
#include <random>
#include <chrono>
#include <cassert>

template <typename T>
static std::vector<int> initialize(const T& input){
    const size_t n = input.size();
    assert((n & (n - 1)) == 0);
    std::vector<int> data(n * 2 - 1);
    for(size_t i = 0; i < n; ++i){
        data[i + n - 1] = input[i];
    }
    for(std::ptrdiff_t i = n - 2; i >= 0; --i){
        data[i] = std::min(data[i * 2 + 1], data[i * 2 + 2]);
    }
    return data;
}

class TopdownSegmentTree {

private:
    std::vector<int> m_data;

    int query_recur(size_t k, size_t a, size_t b, size_t l, size_t r) const {
        if(l <= a && b <= r){
            return m_data[k];
        }else{
            const size_t c = (a + b) / 2;
            int y = std::numeric_limits<int>::max();
            if(l < c && a < r){
                y = std::min(y, query_recur(k * 2 + 1, a, c, l, r));
            }
            if(l < b && c < r){
                y = std::min(y, query_recur(k * 2 + 2, c, b, l, r));
            }
            return y;
        }
    }

public:
    template <typename T>
    explicit TopdownSegmentTree(const T& input)
        : m_data(initialize(input))
    { }

    int query(size_t l, size_t r) const {
        const size_t n = (m_data.size() + 1) / 2;
        return query_recur(0, 0, n, l, r);
    }

};

class BottomupSegmentTree {

private:
    std::vector<int> m_data;

public:
    template <typename T>
    explicit BottomupSegmentTree(const T& input)
        : m_data(initialize(input))
    { }

    int query(size_t l, size_t r) const {
        const size_t n = (m_data.size() + 1) / 2;
        int y = std::numeric_limits<int>::max();
        l += (n - 1);
        r += (n - 1);
        while(l < r){
            if((l & 1u) == 0u){
                y = std::min(y, m_data[l]);
            }
            if((r & 1u) == 0u){
                y = std::min(y, m_data[r - 1]);
            }
            l = l / 2;
            r = (r - 1) / 2;
        }
        return y;
    }

};

void run(size_t log_n, size_t num_queries){
    using duration_type = std::chrono::duration<double>;
    const size_t n = 1 << log_n;
    std::default_random_engine engine;

    std::uniform_int_distribution<int> value_distribution(
        std::numeric_limits<int>::min(), std::numeric_limits<int>::max());
    std::vector<int> init(n);
    for(size_t i = 0; i < n; ++i){
        init[i] = value_distribution(engine);
    }

    std::uniform_int_distribution<size_t> index_distribution(0, n - 1);
    std::vector<std::pair<size_t, size_t>> queries;
    queries.reserve(num_queries);
    for(size_t i = 0; i < num_queries; ++i){
        size_t l = index_distribution(engine);
        size_t r = index_distribution(engine);
        if(l > r){ std::swap(l, r); }
        queries.emplace_back(l, r + 1);
    }

    int td_hash = 0, bu_hash = 0;
    duration_type td_elapsed, bu_elapsed;

    {   // Top-down
        TopdownSegmentTree st(init);
        const auto start = std::chrono::steady_clock::now();
        for(const auto& q : queries){
            td_hash = (td_hash * 11) + st.query(q.first, q.second);
        }
        const auto stop = std::chrono::steady_clock::now();
        td_elapsed = std::chrono::duration_cast<duration_type>(stop - start);
    }

    {   // Bottom-up
        BottomupSegmentTree st(init);
        const auto start = std::chrono::steady_clock::now();
        for(const auto& q : queries){
            bu_hash = (bu_hash * 11) + st.query(q.first, q.second);
        }
        const auto stop = std::chrono::steady_clock::now();
        bu_elapsed = std::chrono::duration_cast<duration_type>(stop - start);
    }

    assert(td_hash == bu_hash);
    std::cout << "Top-down:  " << td_elapsed.count() << " [s]" << std::endl;
    std::cout << "Bottom-up: " << bu_elapsed.count() << " [s]" << std::endl;
    std::cout << "Top-down:  " << (num_queries / td_elapsed.count() / 1e6) << " [Mqps]" << std::endl;
    std::cout << "Bottom-up: " << (num_queries / bu_elapsed.count() / 1e6) << " [Mqps]" << std::endl;
}

int main(){
    for(size_t log_n = 1; log_n <= 28; ++log_n){
        std::cout << "===== n = " << (1ull << log_n) << " =====" << std::endl;
        run(log_n, 10000000);
    }
    return 0;
}

性能評価

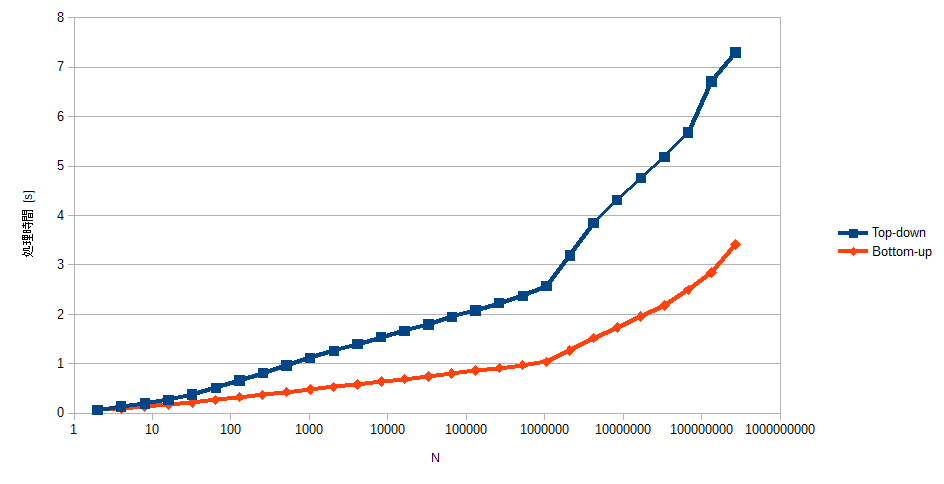
Core i7-4820K上で、数列の要素数$n$を変えながら$10^7$件のランダムなクエリに回答するのにかかった時間を図に示します。
Bottom-upではほぼ全域でTop-downより2倍強ほど高速となっています。

おわりに

書き上げた後に軽く調べたところ、このアルゴリズムは目新しいものというわけでもなく、前から使っている人は使っているようです。（参考: Efficient and easy segment trees）
また、思ったより速くなってしまったので、少しくらい踏み込んで解析したほうがいいかなという気がしています。

定数倍早いコード片は持っておいてもあまり損はしないので、頻繁に使うものは高速化できないかたまに見直してみるのもよいかもしれません。

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。