CoLi-BA: 高速なバンドル調整アルゴリズムの解説（vSLAM, SfM向け高速化手法）

はじめに

ARグラスや自律移動ロボット、ドローンのように、現実世界をカメラで認識しながら動作する技術が進化する中で、カメラの位置や空間中の点群を同時に推定する技術 ー vSLAM (Visual Simultaneous Localization and Mapping) や SfM (Structure from Motion) ー において、高速かつ高精度なバンドル調整（Bundle Adjustment, BA）アルゴリズムは欠かせません。

今回ご紹介する CoLi-BA（Compact Linearization-based Bundle Adjustment）は、2022年にZ. Yeらが発表した、BAソルバです。CoLi-BA では、ヤコビ行列の圧縮による計算時間の短縮、カメラ・特徴点の順序入れ替えによるキャッシュミス率の抑制などを行い、従来手法に比べて高速に計算できるよう様々な工夫がなされています。 実際に、g2o や ceres など従来の広く使われている手法に比べ、精度をさほど落とすことなく 2～5 倍の速さで計算が可能であるとされています。

本文章では、BA 問題の定式化を行った上で、CoLi-BA がどのような手順で計算を行っているか、どの部分が高速化に寄与しているかの解説を行います。

問題の定式化

BA 問題は Tech blog「CUDAによるバンドル調整の高速化とソースコード公開」でも紹介されていますが、より論文の表記に沿った定式化をここで行います。

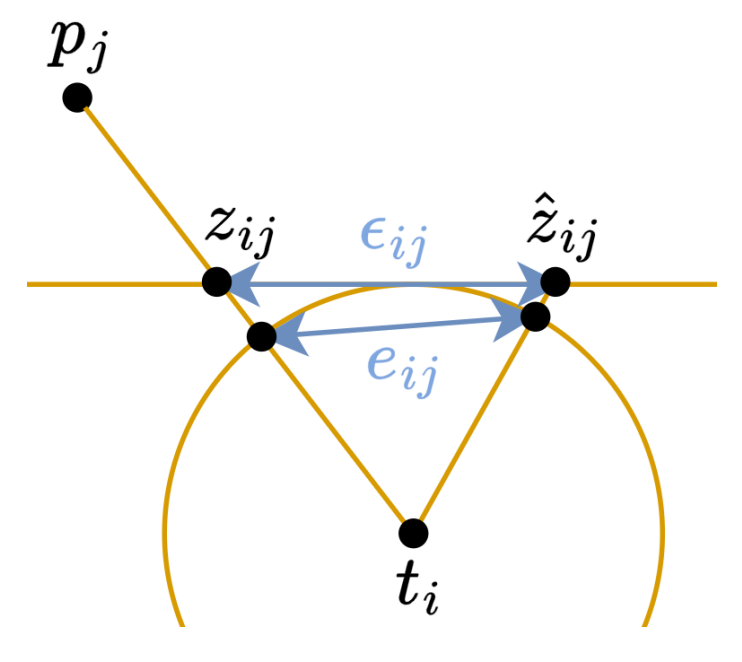
三次元空間中に点群 \({\boldsymbol P} = \{p_j \in {\mathbb R}^3 \mid 1 \leq j \leq n_p\}\) が存在し、これをカメラの集合 \({\boldsymbol C} = \{c_i \mid 1 \leq i \leq n_c\}\) で撮影したとします。 カメラ \(c_i\) の位置 \(t_i \in {\mathbb R}^3\) と回転行列 \(R_i \in \mathcal{M}_{3\times 3}(\mathbb{R})\) を用いて、\(p_j\) を撮影したときの座標 \(z_{ij} \in {\mathbb R}^2\) は以下のように求まります。

1. \(q_{ij} = R_i(p_j – t_i)\) (\(t_i\) からの相対座標に \(R_i\) の回転を施す)
2. 原点と \(q_{ij}\) を通る直線を引き、\(z=1\) 平面と交わる部分の xy 成分を \(z_{ij}\) とする。(つまり、\((x,y,z) \mapsto (x/z,y/z)\) を各点について計算する)

逆に、撮影座標 \(z_{ij}\) が与えられたとき、これを生成するような点群とカメラ位置を知りたいという問題が考えられます。測定誤差 \(\epsilon_{ij}\) を含めた \(\tilde{z}_{ij} = z_{ij} + \epsilon_{ij}\) を入力とし、元の \({\boldsymbol P},{\boldsymbol C}\) を導く問題が BA 問題です。より具体的には、以下のコスト関数

\[ f({\boldsymbol C}, {\boldsymbol P}) = \sum_{1\leq i \leq n_c} \sum_{1 \leq j \leq n_p} \frac{1}{2} ||\epsilon_{ij}||^2 \]

を最小化する \({\boldsymbol C}, {\boldsymbol P}\) を求めることが目標になります。

この問題は非線形最小二乗問題であり、有名なアルゴリズムが知られています。 本文章ではここの手法に関しては深く立ち入らず、必要となる計算である「\(f\) のヘッセ行列を求める」「シューア補行列 (後述) を求める」を CoLi-BA がどのようにして高速化しているかを解説します。 非線形最小二乗問題の解法自体に関してより詳しいことを知りたい方は Tech blog「CUDAによるバンドル調整の高速化とソースコード公開」をご参照ください。

ヤコビ行列の近似

ヘッセ行列を計算するには、まずヤコビ行列の表式を得る必要があります。

\(\epsilon_{ij}\) のヤコビ行列を、カメラの回転・カメラの位置・点の位置の三入力に対応して \(J_{ij} = \begin{pmatrix}J_{ij}^\phi & J_{ij}^t & J_{ij}^p\end{pmatrix}\) と表記します。

補足：ここで、\(\phi_i\) は 3 次元ベクトルで、\(\frac{\partial}{\partial \phi_i}\) は「\(\phi_i\) を軸とした回転に関する偏微分」に対応しています。 この 3 次元ベクトルと 3 次元回転の対応関係は、微小な 3 次元ベクトル \(\omega\) について、\(\omega\) を軸にする微小回転行列を \(I+[\omega]_\times\) と近似できることを利用することによって導出できることが知られています。(https://qiita.com/scomup/items/fa9aed8870585e865117 の「微小回転」「回転の合成」を参照) さらに詳しい解説は、リー群・リー代数に関する資料を参照ください。

各部分は、

\[ J_{ij}^\phi = \frac{\partial \epsilon}{\partial \phi_i} = \frac{\partial \epsilon}{\partial q_{ij}}\frac{\partial q_{ij}}{\partial \phi_i} \] \[ J_{ij}^t = \frac{\partial \epsilon}{\partial t_i} = \frac{\partial \epsilon}{\partial q_{ij}}\frac{\partial q_{ij}}{\partial t_i} \] \[ J_{ij}^p = \frac{\partial \epsilon}{\partial p_j} = \frac{\partial \epsilon}{\partial q_{ij}}\frac{\partial q_{ij}}{\partial p_j} \]

と \(q_{ij}\) を介した二つの偏微分の積として表せます。各式の右側の偏微分は

\[ \frac{\partial q_{ij}}{\partial \phi_i} = -R_i[a_{ij}]_\times \] \[ \frac{\partial q_{ij}}{\partial t_i} = -R_i \] \[ \frac{\partial q_{ij}}{\partial p_j} = R_i \]

と書けます。(ただし、\(a_{ij}\) は \(p_j – t_i\) で、\([a]_\times\) は、\(v\) を \(a \times v\) に写す歪対称行列です。)

一方、左側の偏微分 \(\frac{\partial \epsilon}{\partial q_{ij}}\) の計算は、元の定式化でなされた \(z=1\) 平面への射影ではなく、単位球面への射影上のずれによって測定誤差を近似すると、数式中の行列の性質が良くなり、高速化に寄与することが期待されます。 具体的には、\(\tilde{x}_{ij} = (z_x, z_y, 1)\) (ただし \((z_x, z_y) = \tilde{z}_{ij}\)) として、 \[\epsilon_{ij} \simeq e_{ij} = \frac{q_{ij}}{||q_{ij}||} – \frac{\tilde{x}_{ij}}{||\tilde{x}_{ij}||}\] と近似します。

この近似を入れることで、ヤコビ行列は以下のような表式になります。

\[ J_{ij}^\phi = -R_i[\bar{a}_{ij}]_\times \] \[ J_{ij}^t = -s_{ij}R_i(I-\bar{a}_{ij}\bar{a}_{ij}^\top) \] \[ J_{ij}^p = s_{ij}R_i(I-\bar{a}_{ij}\bar{a}_{ij}^\top) \]

(ただし、\(s_{ij} = \frac{1}{||a_{ij}||}, \bar{a}_{ij} = s_{ij}a_{ij}\))

この式中に登場する行列の性質で、

• \(R_i\) の直交行列性 (逆行列が転置行列)
• \([\bar{a}_{ij}]_\times\) の外積による表現
• \(I – \bar{a}_{ij}\bar{a}_{ij}^\top\) の射影による表現

は今後のヘッセ行列とシューア補行列の構成の高速化に寄与していきます。

ヘッセ行列

次に、コスト関数 \(f\) のヘッセ行列を考えます。 \(N_c = 6n_c, N_p = 3n_p\) として、ヘッセ行列の大きさは \((N_c + N_p) \times (N_c + N_p)\) です。

具体的な表式はヤコビ行列から導出されます。以下の小さなヘッセ行列

\[ H_i^{cc} = \sum_j {J_{ij}^c}^\top J_{ij}^c \] \[ H_j^{pp} = \sum_i {J_{ij}^p}^\top J_{ij}^p \] \[ H_{ij}^{cp} = {J_{ij}^c}^\top J_{ij}^p \]

を定義します。（ただし \(J_{ij}^c = \begin{pmatrix}J_{ij}^\phi & J_{ij}^t\end{pmatrix} \in \mathcal{M}_{3 \times 6} (\mathbb{R})\)）

さらにブロック対角行列 \(A = \text{diag}(H_1^{cc}, \cdots, H_{n_c}^{cc})\) と \(B = \text{diag}(H_1^{pp}, \cdots, H_{n_p}^{pp})\)、ブロック行列 \(D = (H_{ij}^{cp})\) を構成します。すると、全体のヘッセ行列は、

\[ H = \begin{pmatrix} A & D \\ D^\top& B \end{pmatrix} \]

と書けます。

ここで、ヤコビ行列に表れていた回転行列は、ヘッセ行列の表式では消せます。 \(H_j^{pp}\) を例にとると、いくつかの式変形ののち、\(\sum_i s_{ij}^2 (I – \bar{a}_{ij}\bar{a}_{ij}^\top)^\top (I – \bar{a}_{ij}\bar{a}_{ij}^\top)\) となり、確かに \(R_{ij}\) は登場しません。

さらに式は簡略化できます。 \((\bar{a}_{ij}\bar{a}_{ij}^\top)^2 = \bar{a}_{ij}(\bar{a}_{ij}^\top\bar{a}_{ij})\bar{a}_{ij}^\top = \bar{a}_{ij}\bar{a}_{ij}^\top\) に注意すると、 \((I – \bar{a}_{ij}\bar{a}_{ij}^\top)^\top (I – \bar{a}_{ij}\bar{a}_{ij}^\top) = I – 2\bar{a}_{ij}\bar{a}_{ij}^\top + (\bar{a}_{ij}\bar{a}_{ij}^\top)^2 = I – \bar{a}_{ij}\bar{a}_{ij}^\top\) となり、さらに外積の性質 \(\bar{a}_{ij} \times (\bar{a}_{ij} \times x) = (\bar{a}_{ij}^\top x)\bar{a}_{ij} – (\bar{a}_{ij}^\top \bar{a}_{ij})x = (\bar{a}_{ij}\bar{a}_{ij}^\top -I)x\) より、 \(I – \bar{a}_{ij}\bar{a}_{ij}^\top = -[\bar{a}_{ij}]_\times^2\) となります。

最終的に、\(H_j^{pp}\) は \(-s_{ij}^2[\bar{a}_{ij}]_\times^2\) という非常にシンプルな形で表せることがわかりました。

同様の計算で全てのヘッセ行列を書き下すと、ベクトル \(\hat{a}_{ij} = s_{ij}\bar{a}_{ij}\) を用いて以下の表式となることが示せます。

\[ H_i^{cc} = \sum_j \begin{pmatrix} -[\bar{a}_{ij}]_\times^2 & -[\hat{a}_{ij}]_\times \\ [\hat{a}_{ij}]_\times & -[\hat{a}_{ij}]_\times^2 \end{pmatrix} \] \[ H_j^{pp} = \sum_i -[\hat{a}_{ij}]_\times^2 \] \[ H_{ij}^{cp} = \begin{pmatrix} [\hat{a}_{ij}]_\times \\ [\hat{a}_{ij}]_\times^2 \end{pmatrix} \]

シューア補行列

最後に、ヘッセ行列を用いて、シューア補行列というものを計算します。 アルゴリズムでは、ヘッセ行列 \(H\) とある大きなベクトル \(b\) を用いて \(H\varDelta x = b\) の解 \(\varDelta x\) を求める必要があります。

一般には計算量がかかりそうな処理ですが、幸い \(H\) の構造について多くを知っています。特に、\(H = \begin{pmatrix} A & D \\ D^\top& B\end{pmatrix}\) という形で表すことができる場合、シューア補行列 \(A – D B^{-1} D^\top\) を用いることで、\(H\) 全体の逆行列を陽に計算することなく \(\varDelta x\) を計算できます。(詳しくはこちらの Tech blog の「係数行列の構造」を参照してください。)

この計算で、\(B\) はブロック対角行列のため、\(D' := D B^{-1}\) の計算はある程度高速で、ボトルネックになるのは二つの大きな疎行列 \(D' D^\top\) の計算です。\(D'D^\top\) の各ブロックを \(d_{i_1 i_2} \in \mathcal{M}_{3\times 3}(\mathbb{R})\) と定義すると、

\[ d_{i_1i_2} = \sum_j H_{i_1j}^{cp}(H_j^{pp})^{-1}(H_{i_2j}^{cp})^\top \]

と計算できます。ここで前述のヘッセ行列の歪対称行列による表現を用いると、計算の量は格段に減らすことができます。例えば、通常 \(6\times 3\) 行列と \(3\) 次元ベクトルの掛け算は 18 回の乗算を必要としますが、行列 \(H_{ij}^{cp}\) の右側からベクトル \(x\) を掛けた結果は、

\[ H_{ij}^{cp} x = \begin{pmatrix}\hat{a}_{ij} \times x \\ \hat{a}_{ij} \times (\hat{a}_{ij} \times x)\end{pmatrix} \]

より外積 2 回 (乗算 12 回) で計算可能なことがわかります。

こういった工夫をすると、上式の計算において、各 \(j\) で必要な浮動小数点数の積の回数は 162 回から 108 回に落ちることが確かめられます。

順序決定戦略

ここまでの高速化テクニックは、誤差の近似による必要演算回数・メモリ量の削減でした。一方、CoLi-BA ではハードウェアの性質に着目した高速化、具体的にはキャッシュミスを抑制する計算順序の決定も行っています。

現実のデータセットにおいて、多くのカメラと観測点のペアについて依存が無い（観測点がカメラに写っていない）ことが想定されます。 行列 \(D\) の構造はカメラ・観測点間のヘッセ行列を敷き詰めた \(N_c \times N_p\) 行列として表現できますが、依存が無い小行列部分のヘッセ行列は零行列であり、\(D\) はかなり疎であることが見込まれます。（特にカメラが多ければ多いほどこの傾向は強まると予想されます。）

\(D'D^\top\) の各ブロック \(d_{ij}\) を計算する式を再掲すると

\[ d_{i_1i_2} = \sum_j H_{i_1j}^{cp}(H_j^{pp})^{-1}(H_{i_2j}^{cp})^\top \]

ですが、ここで \(j\) は、\(H_{i_1j}^{cp}\) が非零であるようなもののみを見るだけで演算回数が少なくなります。これは \(D\) が疎であることを生かした計算方法であり、既存の手法でも十分に利用されています。 CoLi-BA ではこの高速化に加え、ひとつ前の \(i_1\) で参照した \(H_j^{pp}\) や \(H_{i_2j}^{cp}\) の値がなるべくキャッシュに残るように \(i_1\) の順序を決定することを提案しています。

具体的には、各 \(i\) について \(b^r_i :=\{j \mid H_{ij}^{cp} \neq O\}\) とし、\(1,\cdots, n_c\) の順列 \((o_i)\) であって、\(\sum |b^r_{o_i} \cap b^r_{o_{i+1}}|\) を最小化する問題に定式化を行います。こうして得られた \((o_i)\) の順番で行列の行の順番を入れ替えます。

この問題は \(n_c\) 頂点からなる無向グラフの最小ハミルトン路を求める問題と同一視できます。 よって、厳密解を求めることは難しく、CoLi-BA ではシンプルな貪欲法を用いた近似解から順序を決定しています。

測定結果

元論文では KITTI、1DSfM から選ばれた大小さまざまな 25 個のテストケースについて計測が行われており、ceres と比べて 5 倍、g2o と比べて 2 倍の高速化が達成されている実験結果となっていました。

実際に我々も論文の著者らが公開しているプログラムを 12-core CPU (2.2 GHz) 上で走らせ、実験を行いました。

また、テストケースは、KITTI等のデータを入力として、 ORB-SLAM2を実行したときに計算される BA の入力をダンプすることで作成したものを 10 個用意しました。

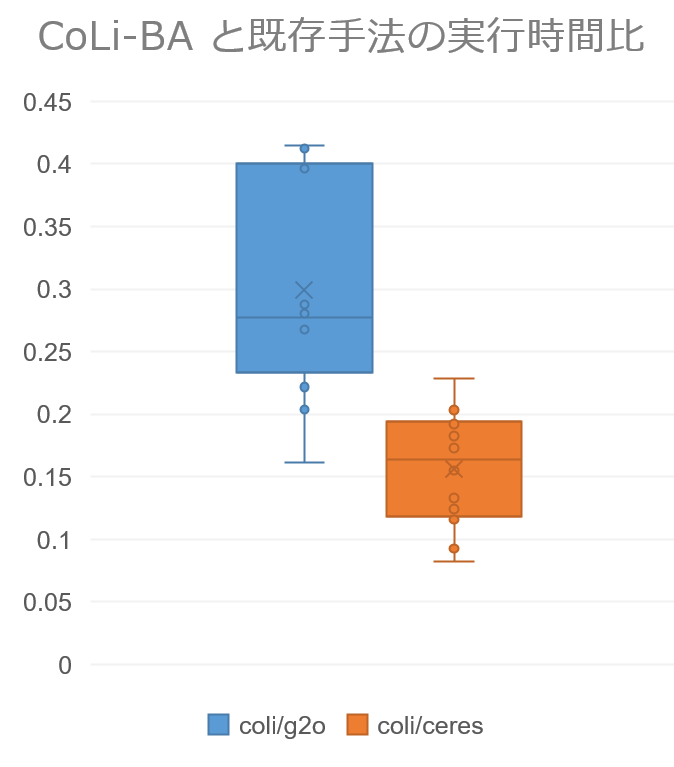
図 1 は各テストケースにおける CoLi-BA の実行時間を、ほかの 2 手法における実行時間で割った値をプロットしています。 テストケース全体の平均としては、g2o に比べて 0.3 倍の時間、ceres に比べて 0.15 倍ほどの時間しかかかっていないことが分かります。

また、CoLi-BA は誤差による近似を行っていることから、既存手法と比べて結果の誤差が乖離していないかも評価する必要があります。

各観測点について、実際の観測座標と、得られた三次元座標から射影される理論上の観測座標の差 \(\epsilon_{ij} = \hat{z}_{ij} – z_{ij}\) の大きさが小さいほど誤差が少ないといえます。 論文では平均二乗誤差

\[ \text{MSE} = \displaystyle \frac{1}{n_c n_p}\sum_{1\leq i \leq n_c} \sum_{1 \leq j \leq n_p} ||\epsilon_{ij}||^2 \]

を誤差評価に用いていたため、ここでもそれに習います。

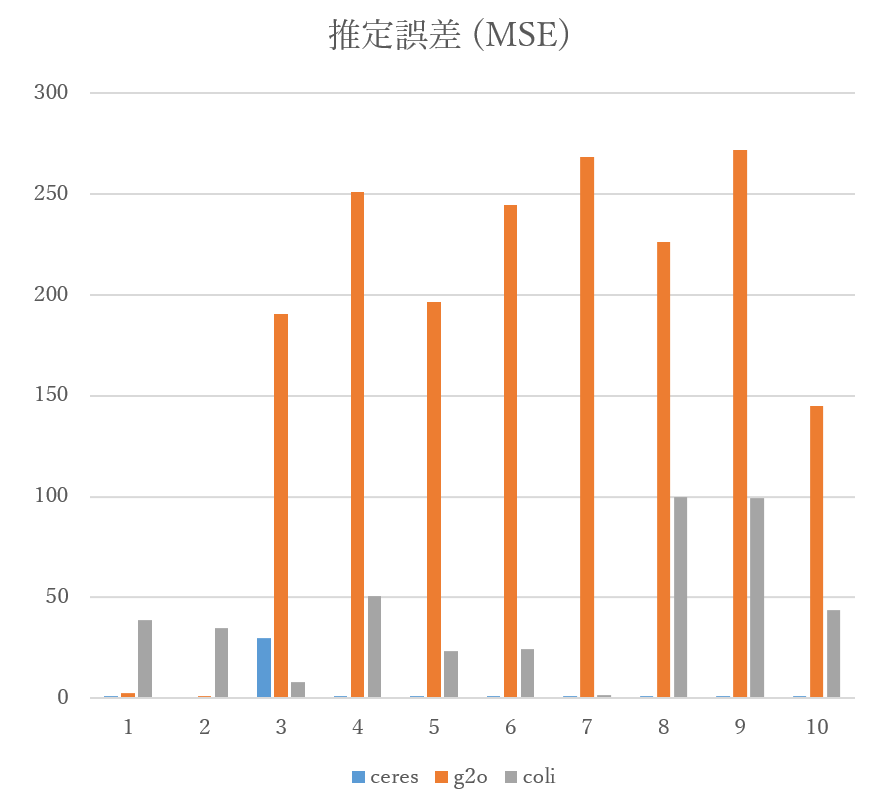
図 2 は各テストケースにおける CoLi-BA、g2o、ceres の平均二乗誤差の大きさを、テストケースの大きさ（カメラ数の大きさ）順に左からプロットしたものです。 いくつかの小さいケースについては、既存手法と比べて CoLi-BA の誤差が大きいことが見て取れますが、中規模程度のテストケースでは g2o の誤差が跳ね上がり、ceres < CoLi-BA < g2o の順番になっています。 論文で試されたテストケース群では誤差にこれほど大規模な差は生まれていないようなので、テストケースの特性（カメラ台数が比較的少ない、など）による手法の得意不得意があることが示唆される結果となりました。

参考文献

• Z. Ye, G. Li, H. Liu, Z. Cui, H. Bao and G. Zhang, “CoLi-BA: Compact Linearization based Solver for Bundle Adjustment,” in IEEE Transactions on Visualization and Computer Graphics, vol. 28, no. 11, pp. 3727-3736, Nov. 2022, doi: 10.1109/TVCG.2022.3203119.

• g2o: https://github.com/RainerKuemmerle/g2o

• ceres: https://github.com/ceres-solver/ceres-solver

This site uses Akismet to reduce spam. Learn how your comment data is processed.