このブログは、株式会社フィックスターズのエンジニアが、あらゆるテーマについて自由に書いているブログです。
Intel AMX (Advanced Matrix Extension) 解説:最適化編
TL;DR
- AMX も、AVX と同じく、性能を引き出すには各種最適化が必要
- 本記事では、Intel Optimization Manual を参考に 4 個の最適化を施し、計算時間を 84% 削減した(理論性能の 87% を達成)
- 最適化の中で、AMX は特にメモリ (TILEDATA) のロード・ストア処理の最適化効果が大きいことが分かった
はじめに
前回の記事では、AMX (Advanced Matrix Extension) の基礎について解説しました。今回は、AMX を活用したコードのさらなる高速化について検証します。特に、大規模行列積演算の性能向上に焦点を当て、比較的簡単にできる具体的な最適化手法とその結果について解説します。
本記事の内容はIntel® 64 and IA-32 Architectures Optimization Reference Manualの20章を参考にしています。このリファレンスでは、以下のような最適化手法が挙げられています。
- ループ順の最適化
- ◎ アキュームレータ数の最適化
- ◎ 命令順最適化
- 畳み込み演算に対する最適化
- ◎ メモリ再配置
- ◎ キャッシュブロッキング
- tileloaddt1を使った最適化
- AVX512とのインターリーブ
- ソフトウェアプリフェッチ
- 転置の最適化
- マルチスレッド化
- 疎な行列積に対する最適化
この記事では、その中から ◎ 記号を付けた次の 4 個の手法を扱います。
- アキュームレータ数の最適化(レジスタブロッキング)
- メモリ再配置
- キャッシュブロッキング
- 命令順最適化
最適化は、単純な行列積演算に対して適用します。行列サイズは 2 通りです。
- 正方行列積(4096×4096 × 4096×4096 => 4096×4096)
- 最適化の適用は、こちらのサイズを例に行います
- Transformer-like(16×4096 × 4096×1920 => 16×1920)
解説のコードを単純化するため、行列サイズはタイルサイズの最大値 16×64 の倍数となるように選んでいます。一般の行列サイズの行列積を計算する場合、端の処理やタイルサイズの決定などについても考える必要があることに注意してください。
実験環境
| 環境 | 設定 |
|---|---|
| OS | Red Hat Enterprise Linux 9.2 |
| CPU | Intel(R) Xeon(R) Platinum 8480CL x2 (56 Core x 2, HT-disabled) |
| メモリ | 512GB (DDR5 32GB x 16) |
| コンパイラ | g++ 14.1.0 |
| コンパイルオプション | -O3 -march=native |
ベースラインコード
本記事では、愚直に実装した正方行列積のコードに対して最適化を適用していきます。つまり、4096×4096 の行列 A と、4096×4096 の行列 B の行列積です。
計算内容は、基礎編のものと同じで、
- 行列Bの要素をAMXのメモリレイアウトに合わせて再配置
- タイルコンフィグを設定
- 16×64ごとのタイルとして
_tile_dpbuud関数で行列積を計算
としています。
この後の最適化で明示的にレジスタを管理するため、前回説明した__tile1024iは使わない方法を使っています。_tile_loadd の第一引数などのAMXの関数に渡すレジスタ番号は式がアセンブリに直接埋め込まれるため、変数や constexpr の値を渡すとエラーになります。そのため、モダンな書き方ではありませんが #define を使ってレジスタ番号を指定しています。
constexpr std::size_t M = 4096;
constexpr std::size_t K = 4096;
constexpr std::size_t N = 4096;
constexpr std::size_t TILE_COLB = 64;
constexpr std::size_t TILE_ROWS = 16;
void ConfigureTILECFG()
{
const TILECFG config = {
.palette_id = 1,
.startRow = 0,
.colb = {TILE_COLB, TILE_COLB, TILE_COLB, TILE_COLB, TILE_COLB, TILE_COLB, TILE_COLB, TILE_COLB},
.rows = {TILE_ROWS, TILE_ROWS, TILE_ROWS, TILE_ROWS, TILE_ROWS, TILE_ROWS, TILE_ROWS, TILE_ROWS},
};
_tile_loadconfig(&config);
}
void ReshapeB(const uint8_t* const B, uint8_t* Bamx)
{
for (int i = 0; i < K; i += 4)
{
for (int j = 0; j < N; j++)
{
const std::uint64_t idx = (i * N) + (j * 4);
Bamx[idx + 0] = B[(i + 0) * N + j];
Bamx[idx + 1] = B[(i + 1) * N + j];
Bamx[idx + 2] = B[(i + 2) * N + j];
Bamx[idx + 3] = B[(i + 3) * N + j];
}
}
return;
}
#define TILEDATA_A1 0
#define TILEDATA_B1 2
#define TILEDATA_C1 4
template <typename T, std::size_t NRow, std::size_t NCol>
struct Tile
{
static constexpr std::size_t tilesInRow = NRow / TILE_ROWS;
static constexpr std::size_t tilesInCol = NCol * sizeof(T) / TILE_COLB;
std::array<std::array<T*, tilesInCol>, tilesInRow> tile_ptr_;
Tile(const T* ptr)
{
constexpr std::size_t bytesInCol = NCol * sizeof(T);
std::uint8_t* p = std::remove_cv_t<std::uint8_t*>(ptr);
// [i][j] tile
for (int i = 0; i < tilesInRow; ++i)
{
for (int j = 0; j < tilesInCol; ++j)
{
const int ii = i * TILE_ROWS;
const int jj = j * TILE_COLB;
tile_ptr_[i][j] = reinterpret_cast<T*>(p + ii * bytesInCol + jj);
}
}
}
auto stride() const -> const std::size_t { return NCol * sizeof(T); }
/**
* @brief Return base ptr of tile[i][j]
*/
auto tile_ptr(const std::size_t i, const std::size_t j) const -> T const* { return tile_ptr_[i][j]; }
};
void GeMMAMX(const uint8_t* const A, const uint8_t* const B, uint32_t* const C)
{
constexpr std::size_t M_TILE = M / TILE_ROWS;
constexpr std::size_t N_TILE = N * sizeof(std::uint32_t) / TILE_COLB;
constexpr std::size_t K_TILE = K * sizeof(std::uint8_t) / TILE_COLB;
ConfigureTILECFG();
auto tileA = Tile<std::uint8_t, M, K>(A);
auto tileB = Tile<std::uint8_t, (K / 4), (N * 4)>(B);
auto tileC = Tile<std::uint32_t, M, N>(C);
for (int i = 0; i < M_TILE; ++i)
{
for (int j = 0; j < N_TILE; ++j)
{
_tile_zero(TILEDATA_C1);
for (int k = 0; k < K_TILE; ++k)
{
_tile_loadd(TILEDATA_A1, tileA.tile_ptr(i, k), tileA.stride());
_tile_loadd(TILEDATA_B1, tileB.tile_ptr(k, j), tileB.stride());
_tile_dpbuud(TILEDATA_C1, TILEDATA_A1, TILEDATA_B1);
}
_tile_stored(TILEDATA_C1, tileC.tile_ptr(i, j), tileC.stride());
}
}
_tile_release();
return;
}
各最適化手法の詳細とコード
レジスタブロッキング
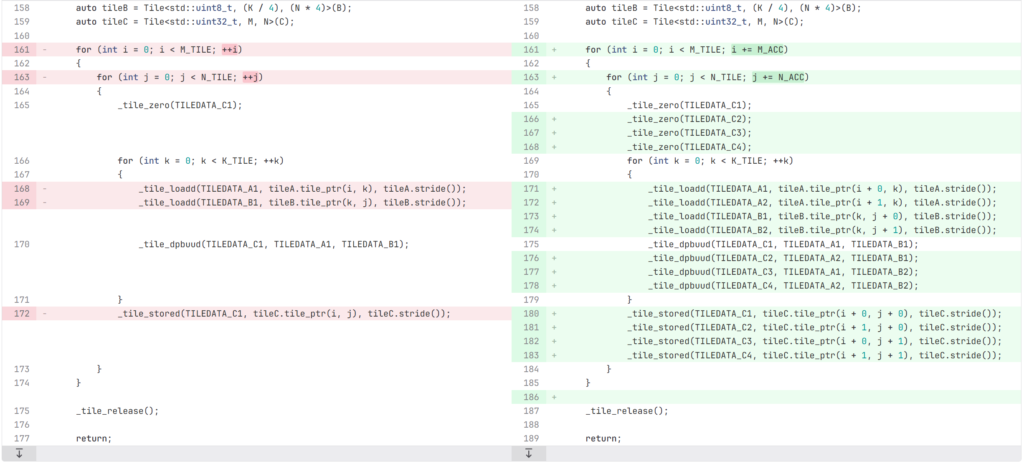
Intel® 64 and IA-32 Architectures Optimization Reference Manualではアキュームレータ数の最適化として説明されています。 これまでのコードでは、8 つの TILEDATA レジスタのうち 3 つしか使っていませんでした。余っているレジスタを使って複数行/列を一気に処理することにより、タイルのロード回数を大幅に減らすことができます。 一度の K 方向のループで、A行列の M_ACC 行と B 行列の N_ACC 列を一気に計算することを考えます。 必要なレジスタ数は、A 行列のタイルに M_ACC 個、B 行列のタイルに N_ACC 個、C行列のタイルに M_ACC * N_ACC 個で、合計 M_ACC*N_ACC + M_ACC + N_ACC 個です。(計算順を工夫することにより A と B どちらかのタイルとして一つのレジスタを使いまわすことができ、正確には M_ACC*N_ACC + min(M_ACC, N_ACC) + 1 個にできます。)
次にタイルのロード回数を考えます。元の方法では、A行列、B行列それぞれ K 回ずつ、つまり行列積全体で 2MNK 回のロードが必要でした。 一方、一気に計算する場合では、一度のループで A 行列のロードが M_ACC * K 回、B行列が N_ACC * K 回必要ですが、ループ回数が M*N/(M_ACC * N_ACC) 回に減るため、行列積全体では MNK(M_ACC + N_ACC)/(M_ACC*N_ACC) 回となります。 レジスタ数に関する条件 (M_ACC * N_ACC) + M_ACC + N_ACC ≦ 8 を満たす中でロード回数を最小化するには、M_ACC = 2 N_ACC = 2 とすればよいです。このとき、MNK(M_ACC + N_ACC)/(M_ACC*N_ACC) = MNKとなるため、ロード回数が元の半分になることがわかります。
この場合、一度に処理する行数は 1 タイルの行数なので 16 * M_ACC = 32 行となりますが、 Transformer-like の場合など M が 32 より小さい場合これは過剰です。この場合、M_ACC = 1, N_ACC = 6 とすることで効率的になります。
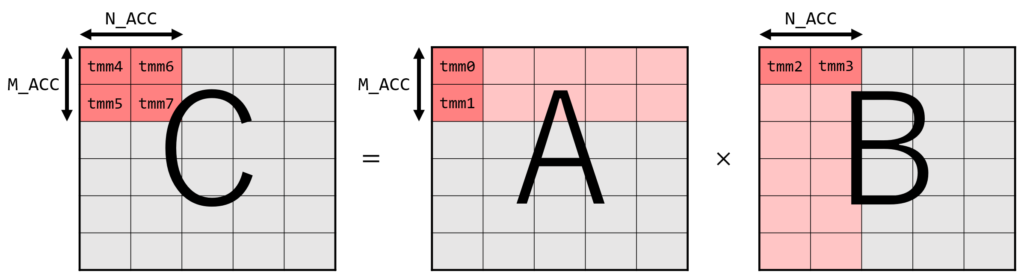
constexpr std::size_t M_ACC = 2;
constexpr std::size_t N_ACC = 2;
#define TILEDATA_A1 0
#define TILEDATA_A2 1
#define TILEDATA_B1 2
#define TILEDATA_B2 3
#define TILEDATA_C1 4
#define TILEDATA_C2 5
#define TILEDATA_C3 6
#define TILEDATA_C4 7
void GeMMAMX(const uint8_t* const A, const uint8_t* const B, uint32_t* const C)
{
constexpr std::size_t M_TILE = M / TILE_ROWS;
constexpr std::size_t N_TILE = N * sizeof(std::uint32_t) / TILE_COLB;
constexpr std::size_t K_TILE = K * sizeof(std::uint8_t) / TILE_COLB;
ConfigureTILECFG();
auto tileA = Tile<std::uint8_t, M, K>(A);
auto tileB = Tile<std::uint8_t, (K / 4), (N * 4)>(B);
auto tileC = Tile<std::uint32_t, M, N>(C);
for (int i = 0; i < M_TILE; i += M_ACC)
{
for (int j = 0; j < N_TILE; j += N_ACC)
{
_tile_zero(TILEDATA_C1);
_tile_zero(TILEDATA_C2);
_tile_zero(TILEDATA_C3);
_tile_zero(TILEDATA_C4);
for (int k = 0; k < K_TILE; ++k)
{
_tile_loadd(TILEDATA_A1, tileA.tile_ptr(i + 0, k), tileA.stride());
_tile_loadd(TILEDATA_A2, tileA.tile_ptr(i + 1, k), tileA.stride());
_tile_loadd(TILEDATA_B1, tileB.tile_ptr(k, j + 0), tileB.stride());
_tile_loadd(TILEDATA_B2, tileB.tile_ptr(k, j + 1), tileB.stride());
_tile_dpbuud(TILEDATA_C1, TILEDATA_A1, TILEDATA_B1);
_tile_dpbuud(TILEDATA_C2, TILEDATA_A2, TILEDATA_B1);
_tile_dpbuud(TILEDATA_C3, TILEDATA_A1, TILEDATA_B2);
_tile_dpbuud(TILEDATA_C4, TILEDATA_A2, TILEDATA_B2);
}
_tile_stored(TILEDATA_C1, tileC.tile_ptr(i + 0, j + 0), tileC.stride());
_tile_stored(TILEDATA_C2, tileC.tile_ptr(i + 1, j + 0), tileC.stride());
_tile_stored(TILEDATA_C3, tileC.tile_ptr(i + 0, j + 1), tileC.stride());
_tile_stored(TILEDATA_C4, tileC.tile_ptr(i + 1, j + 1), tileC.stride());
}
}
_tile_release();
return;
}
メモリ再配置
AMX はタイル構造でデータを処理するため、メモリレイアウトが性能に大きく影響します。タイルごとに連続したメモリ位置に配置し、行列積で計算する順番に合わせて並べることによってハードウェアプリフェッチしやすく、キャッシュに乗りやすくなります。 ただし、並び変えのオーバーヘッドがかかるため行列が小さい場合はむしろ遅くなってしまいます。
例えば正方行列積の場合、レジスタブロッキングの章で述べた通りA行列は M_ACC = 2 行ごとにまとめて計算するため、以下の図のような順番でタイルを 2 行ごとに配置します。B行列も N_ACC = 2 で同様です。
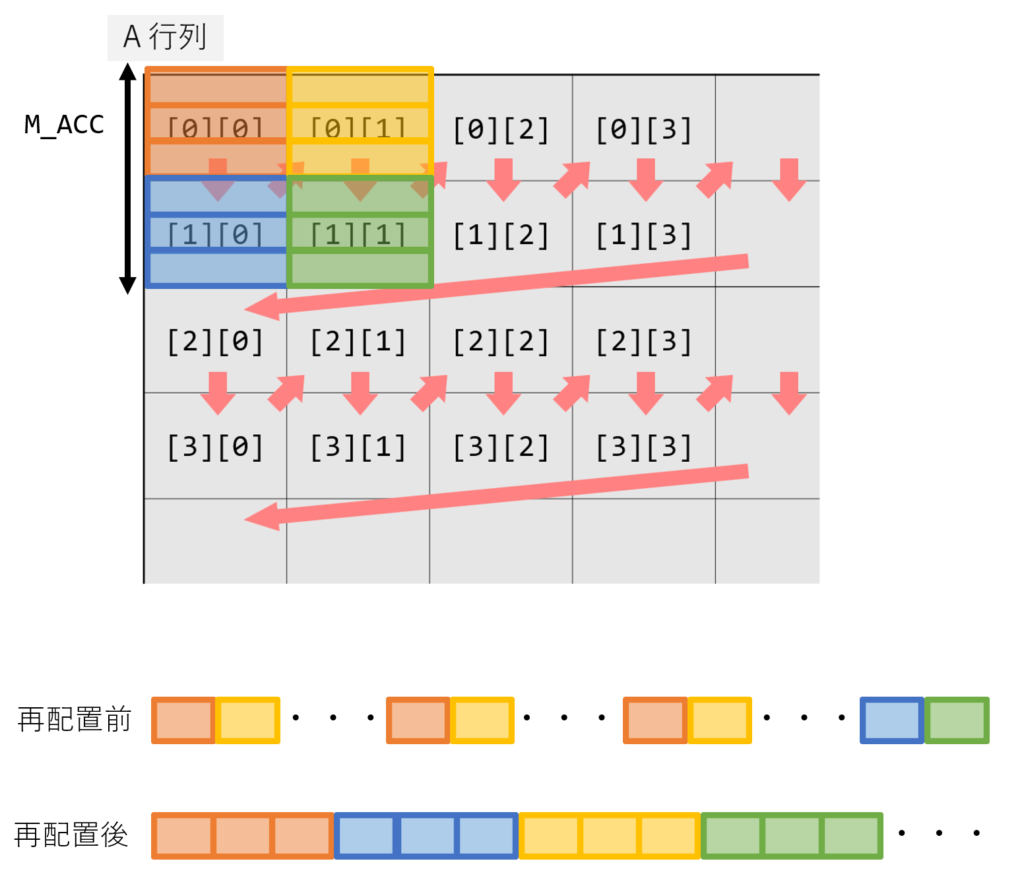
具体的な計算としては、一度 TILE をロードした後、連続領域になるようにストアします。
void RelayoutA(const uint8_t* const A, uint8_t* Aamx)
{
constexpr std::size_t tilesInRow = M / TILE_ROWS;
constexpr std::size_t tilesInCol = K * sizeof(std::uint8_t) / TILE_COLB;
auto tileA = Tile<std::uint8_t, M, K>(A);
std::uint8_t* p = std::remove_cv_t<std::uint8_t*>(Aamx);
for (int m = 0; m < tilesInRow; m += M_ACC)
{
for (int k = 0; k < tilesInCol; ++k)
{
for (int i = 0; i < M_ACC; ++i)
{
const std::size_t mm = m + i;
const std::size_t kk = k;
_tile_loadd(TILEDATA_A1, tileA.tile_ptr(mm, kk), tileA.stride());
_tile_stored(TILEDATA_A1, p, TILE_COLB);
p += (TILE_ROWS * TILE_COLB);
}
}
}
return;
}
void RelayoutB(const uint8_t* const B, uint8_t* Bamx)
{
constexpr std::size_t tilesInRow = (K / 4) / TILE_ROWS;
constexpr std::size_t tilesInCol = (N * 4) * sizeof(std::uint8_t) / TILE_COLB;
auto tileB = Tile<std::uint8_t, (K / 4), (N * 4)>(B);
std::uint8_t* p = std::remove_cv_t<std::uint8_t*>(Bamx);
for (int n = 0; n < tilesInCol; n += N_ACC)
{
for (int k = 0; k < tilesInRow; ++k)
{
for (int i = 0; i < N_ACC; ++i)
{
const std::size_t kk = k;
const std::size_t nn = n + i;
_tile_loadd(TILEDATA_B1, tileB.tile_ptr(kk, nn), tileB.stride());
_tile_stored(TILEDATA_B1, p, TILE_COLB);
p += (TILE_ROWS * TILE_COLB);
}
}
}
return;
}
template <typename T, std::size_t NRow, std::size_t NCol>
struct TileA
{
static constexpr std::size_t tilesInRow = NRow / TILE_ROWS;
static constexpr std::size_t tilesInCol = NCol * sizeof(T) / TILE_COLB;
std::array<std::array<T*, tilesInCol>, tilesInRow> tile_ptr_;
TileA(const T* ptr)
{
std::uint8_t* p = std::remove_cv_t<std::uint8_t*>(ptr);
// [i][j] tile
for (int m = 0; m < tilesInRow; m += M_ACC)
{
for (int k = 0; k < tilesInCol; ++k)
{
for (int i = 0; i < M_ACC; ++i)
{
const std::size_t mm = m + i;
const std::size_t kk = k;
tile_ptr_[mm][kk] = p;
p += (TILE_ROWS * TILE_COLB);
}
}
}
}
auto stride() const -> const std::size_t { return TILE_COLB; }
/**
* @brief Return base ptr of tile[i][j]
*/
auto tile_ptr(const std::size_t i, const std::size_t j) const -> T const* { return tile_ptr_[i][j]; }
};
template <typename T, std::size_t NRow, std::size_t NCol>
struct TileB
{
static constexpr std::size_t tilesInRow = NRow / TILE_ROWS;
static constexpr std::size_t tilesInCol = NCol * sizeof(T) / TILE_COLB;
std::array<std::array<T*, tilesInCol>, tilesInRow> tile_ptr_;
TileB(const T* ptr)
{
std::uint8_t* p = std::remove_cv_t<std::uint8_t*>(ptr);
// [i][j] tile
for (int n = 0; n < tilesInCol; n += N_ACC)
{
for (int k = 0; k < tilesInRow; ++k)
{
for (int i = 0; i < N_ACC; ++i)
{
const std::size_t kk = k;
const std::size_t nn = n + i;
tile_ptr_[kk][nn] = p;
p += (TILE_ROWS * TILE_COLB);
}
}
}
}
auto stride() const -> const std::size_t { return TILE_COLB; }
/**
* @brief Return base ptr of tile[i][j]
*/
auto tile_ptr(const std::size_t i, const std::size_t j) const -> T const* { return tile_ptr_[i][j]; }
};
void GeMMAMX(const uint8_t* const A, const uint8_t* const B, uint32_t* const C)
{
constexpr std::size_t M_TILE = M / TILE_ROWS;
constexpr std::size_t N_TILE = N * sizeof(std::uint32_t) / TILE_COLB;
constexpr std::size_t K_TILE = K * sizeof(std::uint8_t) / TILE_COLB;
ConfigureTILECFG();
auto tileA = TileA<std::uint8_t, M, K>(A);
auto tileB = TileB<std::uint8_t, (K / 4), (N * 4)>(B);
auto tileC = Tile<std::uint32_t, M, N>(C);
for (int i = 0; i < M_TILE; i += M_ACC)
{
for (int j = 0; j < N_TILE; j += N_ACC)
{
_tile_zero(TILEDATA_C1);
_tile_zero(TILEDATA_C2);
_tile_zero(TILEDATA_C3);
_tile_zero(TILEDATA_C4);
for (int k = 0; k < K_TILE; ++k)
{
_tile_loadd(TILEDATA_A1, tileA.tile_ptr(i + 0, k), tileA.stride());
_tile_loadd(TILEDATA_A2, tileA.tile_ptr(i + 1, k), tileA.stride());
_tile_loadd(TILEDATA_B1, tileB.tile_ptr(k, j + 0), tileB.stride());
_tile_loadd(TILEDATA_B2, tileB.tile_ptr(k, j + 1), tileB.stride());
_tile_dpbuud(TILEDATA_C1, TILEDATA_A1, TILEDATA_B1);
_tile_dpbuud(TILEDATA_C2, TILEDATA_A2, TILEDATA_B1);
_tile_dpbuud(TILEDATA_C3, TILEDATA_A1, TILEDATA_B2);
_tile_dpbuud(TILEDATA_C4, TILEDATA_A2, TILEDATA_B2);
}
_tile_stored(TILEDATA_C1, tileC.tile_ptr(i + 0, j + 0), tileC.stride());
_tile_stored(TILEDATA_C2, tileC.tile_ptr(i + 1, j + 0), tileC.stride());
_tile_stored(TILEDATA_C3, tileC.tile_ptr(i + 0, j + 1), tileC.stride());
_tile_stored(TILEDATA_C4, tileC.tile_ptr(i + 1, j + 1), tileC.stride());
}
}
_tile_release();
return;
}

キャッシュブロッキング
AVX を使った行列積の計算と同様に、適切なサイズでキャッシュブロッキングすることによってキャッシュを最適化することができます。K 方向のブロッキングは、C 行列のロード・ストアが増加するため、推奨されません。特に uint8_t の行列積は uint32_t で集計されるため、K 方向のブロッキングでロード・ストアされるデータ量が大幅に増加 します。行列サイズと CPU のキャッシュサイズによって適切なブロッキングの幅は異なるため、実際に実行時間をベンチしながら決めるのが良さそうです。
今回 K 方向が 4096 あるため、L1 キャッシュには収まりません。L2 キャッシュに収めるため、正方行列積の場合は M 方向に 16 タイル、N 方向に 4 タイルでブロッキングしています。
Transformer-like の場合は M が小さく、M 方向のループが存在しないため、ブロッキングは不要です。
constexpr std::size_t M_CACHE = 16;
constexpr std::size_t N_CACHE = 4;
void GeMMAMX(const uint8_t* const A, const uint8_t* const B, uint32_t* const C)
{
constexpr std::size_t M_TILE = M / TILE_ROWS;
constexpr std::size_t N_TILE = N * sizeof(std::uint32_t) / TILE_COLB;
constexpr std::size_t K_TILE = K * sizeof(std::uint8_t) / TILE_COLB;
ConfigureTILECFG();
auto tileA = TileA<std::uint8_t, M, K>(A);
auto tileB = TileB<std::uint8_t, (K / 4), (N * 4)>(B);
auto tileC = Tile<std::uint32_t, M, N>(C);
for (int ib = 0; ib < M_TILE; ib += M_CACHE)
{
for (int jb = 0; jb < N_TILE; jb += N_CACHE)
{
for (int i = ib; i < ib + M_CACHE; i += M_ACC)
{
for (int j = jb; j < jb + N_CACHE; j += N_ACC)
{
_tile_zero(TILEDATA_C1);
_tile_zero(TILEDATA_C2);
_tile_zero(TILEDATA_C3);
_tile_zero(TILEDATA_C4);
for (int k = 0; k < K_TILE; ++k)
{
_tile_loadd(TILEDATA_A1, tileA.tile_ptr(i + 0, k), tileA.stride());
_tile_loadd(TILEDATA_A2, tileA.tile_ptr(i + 1, k), tileA.stride());
_tile_loadd(TILEDATA_B1, tileB.tile_ptr(k, j + 0), tileB.stride());
_tile_loadd(TILEDATA_B2, tileB.tile_ptr(k, j + 1), tileB.stride());
_tile_dpbuud(TILEDATA_C1, TILEDATA_A1, TILEDATA_B1);
_tile_dpbuud(TILEDATA_C2, TILEDATA_A2, TILEDATA_B1);
_tile_dpbuud(TILEDATA_C3, TILEDATA_A1, TILEDATA_B2);
_tile_dpbuud(TILEDATA_C4, TILEDATA_A2, TILEDATA_B2);
}
_tile_stored(TILEDATA_C1, tileC.tile_ptr(i + 0, j + 0), tileC.stride());
_tile_stored(TILEDATA_C2, tileC.tile_ptr(i + 1, j + 0), tileC.stride());
_tile_stored(TILEDATA_C3, tileC.tile_ptr(i + 0, j + 1), tileC.stride());
_tile_stored(TILEDATA_C4, tileC.tile_ptr(i + 1, j + 1), tileC.stride());
}
}
}
}
_tile_release();
return;
}
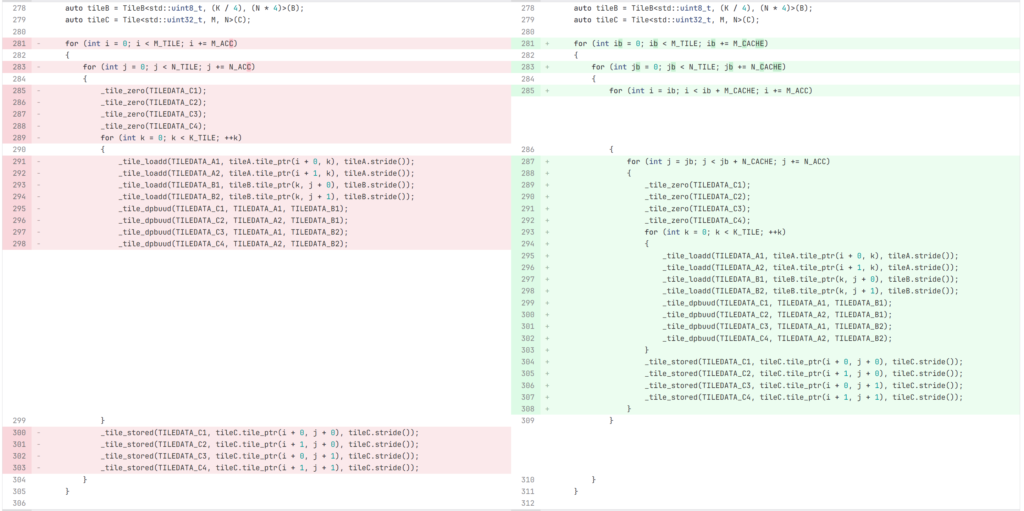
命令順最適化
tileloadd と tilestored 命令を tdpbuud 命令でインターリーブすることにより、CPU のパイプラインを最大限に活用することができます。if文は適切に最適化オプションをつけるとコンパイラによって展開されます。
void GeMMAMX(const uint8_t* const A, const uint8_t* const B, uint32_t* const C)
{
constexpr std::size_t M_TILE = M / TILE_ROWS;
constexpr std::size_t N_TILE = N * sizeof(std::uint32_t) / TILE_COLB;
constexpr std::size_t K_TILE = K * sizeof(std::uint8_t) / TILE_COLB;
ConfigureTILECFG();
auto tileA = TileA<std::uint8_t, M, K>(A);
auto tileB = TileB<std::uint8_t, (K / 4), (N * 4)>(B);
auto tileC = Tile<std::uint32_t, M, N>(C);
for (int ib = 0; ib < M_TILE; ib += M_CACHE)
{
for (int jb = 0; jb < N_TILE; jb += N_CACHE)
{
for (int i = ib; i < ib + M_CACHE; i += M_ACC)
{
for (int j = jb; j < jb + N_CACHE; j += N_ACC)
{
for (int k = 0; k < K_TILE; ++k)
{
_tile_loadd(TILEDATA_A1, tileA.tile_ptr(i + 0, k), tileA.stride());
_tile_loadd(TILEDATA_B1, tileB.tile_ptr(k, j + 0), tileB.stride());
if (k == 0)
{
_tile_zero(TILEDATA_C1);
}
_tile_dpbuud(TILEDATA_C1, TILEDATA_A1, TILEDATA_B1);
if (k == (K_TILE - 1))
{
_tile_stored(TILEDATA_C1, tileC.tile_ptr(i + 0, j + 0), tileC.stride());
}
_tile_loadd(TILEDATA_A2, tileA.tile_ptr(i + 1, k), tileA.stride());
if (k == 0)
{
_tile_zero(TILEDATA_C2);
}
_tile_dpbuud(TILEDATA_C2, TILEDATA_A2, TILEDATA_B1);
if (k == (K_TILE - 1))
{
_tile_stored(TILEDATA_C2, tileC.tile_ptr(i + 1, j + 0), tileC.stride());
}
_tile_loadd(TILEDATA_B2, tileB.tile_ptr(k, j + 1), tileB.stride());
if (k == 0)
{
_tile_zero(TILEDATA_C3);
}
_tile_dpbuud(TILEDATA_C3, TILEDATA_A1, TILEDATA_B2);
if (k == (K_TILE - 1))
{
_tile_stored(TILEDATA_C3, tileC.tile_ptr(i + 0, j + 1), tileC.stride());
}
if (k == 0)
{
_tile_zero(TILEDATA_C4);
}
_tile_dpbuud(TILEDATA_C4, TILEDATA_A2, TILEDATA_B2);
if (k == (K_TILE - 1))
{
_tile_stored(TILEDATA_C4, tileC.tile_ptr(i + 1, j + 1), tileC.stride());
}
}
}
}
}
}
_tile_release();
return;
}

Transformer-like の場合の最終的なコードは次のようになります。
#define TILEDATA_A1 0
#define TILEDATA_B1 1
#define TILEDATA_C1 2
#define TILEDATA_C2 3
#define TILEDATA_C3 4
#define TILEDATA_C4 5
#define TILEDATA_C5 6
#define TILEDATA_C6 7
constexpr std::size_t N_ACC = 6;
void GeMMAMX(const uint8_t* const A, const uint8_t* const B, uint32_t* const C)
{
constexpr std::size_t M_TILE = M / TILE_ROWS;
constexpr std::size_t N_TILE = N * sizeof(std::uint32_t) / TILE_COLB;
constexpr std::size_t K_TILE = K * sizeof(std::uint8_t) / TILE_COLB;
ConfigureTILECFG();
auto tileA = TileA<std::uint8_t, M, K>(A);
auto tileB = TileB<std::uint8_t, (K / 4), (N * 4)>(B);
auto tileC = Tile<std::uint32_t, M, N>(C);
for (int i = 0; i < M_TILE; ++i)
{
for (int jb = 0; jb < N_TILE; jb += N_CACHE)
{
for (int j = jb; j < jb + N_CACHE; j += N_ACC)
{
for (int k = 0; k < K_TILE; ++k)
{
_tile_loadd(TILEDATA_A1, tileA.tile_ptr(i + 0, k), tileA.stride());
// j + 0
_tile_loadd(TILEDATA_B1, tileB.tile_ptr(k, j + 0), tileB.stride());
if (k == 0)
{
_tile_zero(TILEDATA_C1);
}
_tile_dpbuud(TILEDATA_C1, TILEDATA_A1, TILEDATA_B1);
if (k == (K_TILE - 1))
{
_tile_stored(TILEDATA_C1, tileC.tile_ptr(i + 0, j + 0), tileC.stride());
}
// j + 1
_tile_loadd(TILEDATA_B1, tileB.tile_ptr(k, j + 1), tileA.stride());
if (k == 0)
{
_tile_zero(TILEDATA_C2);
}
_tile_dpbuud(TILEDATA_C2, TILEDATA_A1, TILEDATA_B1);
if (k == (K_TILE - 1))
{
_tile_stored(TILEDATA_C2, tileC.tile_ptr(i, j + 1), tileC.stride());
}
// j + 2
_tile_loadd(TILEDATA_B1, tileB.tile_ptr(k, j + 2), tileA.stride());
if (k == 0)
{
_tile_zero(TILEDATA_C3);
}
_tile_dpbuud(TILEDATA_C3, TILEDATA_A1, TILEDATA_B1);
if (k == (K_TILE - 1))
{
_tile_stored(TILEDATA_C3, tileC.tile_ptr(i, j + 2), tileC.stride());
}
// j + 3
_tile_loadd(TILEDATA_B1, tileB.tile_ptr(k, j + 3), tileA.stride());
if (k == 0)
{
_tile_zero(TILEDATA_C4);
}
_tile_dpbuud(TILEDATA_C4, TILEDATA_A1, TILEDATA_B1);
if (k == (K_TILE - 1))
{
_tile_stored(TILEDATA_C4, tileC.tile_ptr(i, j + 3), tileC.stride());
}
// j + 4
_tile_loadd(TILEDATA_B1, tileB.tile_ptr(k, j + 4), tileA.stride());
if (k == 0)
{
_tile_zero(TILEDATA_C5);
}
_tile_dpbuud(TILEDATA_C5, TILEDATA_A1, TILEDATA_B1);
if (k == (K_TILE - 1))
{
_tile_stored(TILEDATA_C5, tileC.tile_ptr(i, j + 4), tileC.stride());
}
// j + 5
_tile_loadd(TILEDATA_B1, tileB.tile_ptr(k, j + 5), tileA.stride());
if (k == 0)
{
_tile_zero(TILEDATA_C6);
}
_tile_dpbuud(TILEDATA_C6, TILEDATA_A1, TILEDATA_B1);
if (k == (K_TILE - 1))
{
_tile_stored(TILEDATA_C6, tileC.tile_ptr(i, j + 5), tileC.stride());
}
}
}
}
}
_tile_release();
return;
}
実験結果
以下の表は、正方行列積に対して各最適化手法を適用した場合の実行時間(ms)を示します。それぞれ一つ上までの最適化に追加で適用した際の実行時間を表します。 実行時間は tilecfg 関数の呼び出し前から _tile_release の呼び出し後までの区間で計測しています。メモリの確保、解放、再配置はあらかじめ行われているという状況を想定し、これらの時間は含めていません。
| 最適化手法 | 実行時間 [ms] | GFLOPS | 改善率 [%] |
|---|---|---|---|
| ベースライン | 385.03 | 357 | – |
| + レジスタブロッキング | 137.84 | 997 | 64 |
| + メモリ再配置 | 106.94 | 1285 | 72 |
| + キャッシュブロッキング | 61.99 | 2217 | 84 |
| + 命令順最適化 | 61.39 | 2239 | 84 |
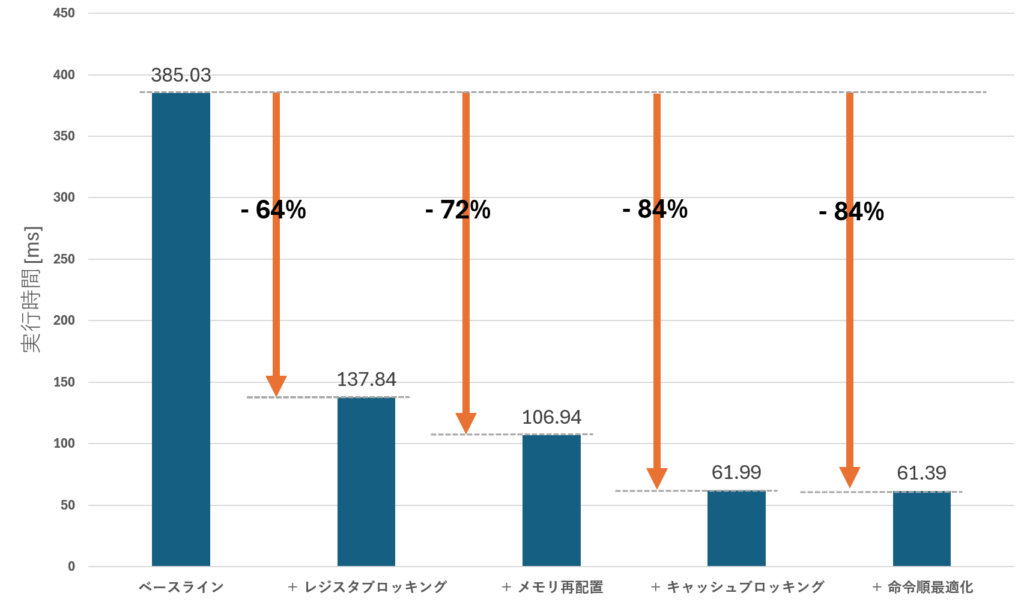
各手法を単体で適用した結果は次の通りです。命令順最適化についてはレジスタブロッキングを前提としているため省略します。
レジスタブロッキングとメモリ再配置の効果が大きく、キャッシュブロッキングは単体では効果が小さいことが分かります。つまり、AMX ではレジスタ TILEDATA のロード・ストア処理が支配的であり、強く意識して最適化する必要があることが分かります。
| 最適化手法 | 実行時間 [ms] | GFLOPS | 改善率 [%] |
|---|---|---|---|
| ベースライン | 360.13 | 389 | – |
| レジスタブロッキング | 131.90 | 1098 | 63 |
| メモリ再配置 | 199.12 | 775 | 45 |
| キャッシュブロッキング | 343.91 | 412 | 5 |
Transformer-like の場合は以下の通りです。
最適化の効果は見えますが、計算サイズが小さい影響か GFLOPS の値は小さいままです。
| 最適化手法 | 実行時間 [ms] | GFLOPS | 改善率 [%] |
|---|---|---|---|
| ベースライン | 0.69 | 365 | – |
| 全部 | 0.31 | 812 | 56% |
考察
AMX 行列積の 1 スレッド理論性能は 2867 GFLOPS です(実測した動作周波数を使用しているため、基礎編とは値が異なります)。今回の最終的なコードは 2239 GFLOPSと、理論性能の 84% 程度の性能達成しました。 レジスタブロッキングは命令数の削減に直接寄与しており、単体でも 64% の改善が見られるため、特に重要であると言えそうです。一方、命令順最適化についてはほとんど高速化に寄与していないようでした。メモリ再配置は単体でも 45% の改善率となり、ハードウェアプリフェッチが効果的であることも分かりました。 ソフトウェアプリフェッチなどのこの記事で紹介していない高速化を用いることでさらなる高速化も望めるようです。 命令数の削減・命令順の最適化など、AVX で有用だった最適化方法が依然有用である上で、一度に扱うデータのサイズが大きい分メモリバウンドとなりやすく、キャッシュブロッキングやメモリ再配置などの工夫がより重要となっていると言えると思います。
まとめ
本記事では、AMXを使った行列積の四つの高速化手法について解説・検証しました。 最終的には、ベースライン実装から正方行列積の場合で 84%、Transformer-likeの場合で 56% の高速化が達成できました。
参考文献
- Intel® 64 and IA-32 Architectures Optimization Reference Manual:
Volume 1, https://www.intel.co.jp/content/www/jp/ja/content-details/671488/intel-64-and-ia-32-architectures-optimization-reference-manual-volume-1.html - GitHub – usstq/mm_amx, https://github.com/usstq/mm_amx/tree/master
- Tips to Measure the Performance of Matrix Multiplication Using
oneMKL, https://www.intel.com/content/www/us/en/developer/articles/technical/a-simple-example-to-measure-the-performance-of-an-intel-mkl-function.html
Tags
Leave a Comment
Tags
Archives
- 2026年2月
- 2026年1月
- 2025年12月
- 2025年11月
- 2025年8月
- 2025年5月
- 2025年4月
- 2024年11月
- 2024年10月
- 2024年7月
- 2024年5月
- 2024年4月
- 2024年2月
- 2024年1月
- 2023年12月
- 2023年6月
- 2023年5月
- 2023年4月
- 2023年2月
- 2023年1月
- 2022年12月
- 2022年10月
- 2021年11月
- 2021年9月
- 2021年6月
- 2021年3月
- 2021年2月
- 2020年12月
- 2020年10月
- 2020年7月
- 2020年6月
- 2020年5月
- 2020年4月
- 2020年3月
- 2020年2月
- 2020年1月
- 2019年12月
- 2019年11月
- 2019年10月
- 2019年9月
- 2019年8月
- 2019年6月
- 2019年4月
- 2019年3月
- 2019年2月
- 2019年1月
- 2018年12月
- 2018年11月
- 2018年10月
- 2018年8月
- 2018年6月
- 2018年5月
- 2018年4月
- 2018年3月
- 2018年2月
- 2017年12月
- 2017年11月
- 2017年10月
- 2017年9月
- 2017年8月
- 2017年7月
- 2017年6月
- 2017年5月
- 2017年3月
- 2016年12月
- 2016年11月
- 2016年8月
- 2016年7月
- 2016年3月
- 2016年2月
- 2016年1月
- 2015年12月
- 2015年11月
- 2015年10月
- 2015年8月
- 2015年6月
- 2015年3月
- 2015年2月
- 2015年1月
- 2014年12月
- 2014年11月



keisuke.kimura in Livox Mid-360をROS1/ROS2で動かしてみた
Sorry for the delay in replying. I have done SLAM (FAST_LIO) with Livox MID360, but for various reasons I have not be...
Miya in ウエハースケールエンジン向けSimulated Annealingを複数タイルによる並列化で実装しました
作成されたプロファイラがとても良さそうです :) ぜひ詳細を書いていただきたいです!...
Deivaprakash in Livox Mid-360をROS1/ROS2で動かしてみた
Hey guys myself deiva from India currently i am working in this Livox MID360 and eager to knwo whether you have done the...
岩崎システム設計 岩崎 満 in Alveo U50で10G Ethernetを試してみる
仕事の都合で、検索を行い、御社サイトにたどりつきました。 内容は大変参考になりま�...
Prabuddhi Wariyapperuma in Livox Mid-360をROS1/ROS2で動かしてみた
This issue was sorted....