このブログは、株式会社フィックスターズのエンジニアが、あらゆるテーマについて自由に書いているブログです。
3D Gaussian Splatting を約 40 % 高速化した話
はじめに
アルバイトの星井です.
本記事は,3D Gaussian Splatting の高速化の成果報告です.
以前にも本サイト(3D Gaussian Splatting の紹介と高速化)にて 3D Gaussian Splatting の高速化についての報告を紹介しましたが, この時は全体の処理時間に対して 約 4 % 程度の高速化でしたが,今回は約 40 % の高速化を達成しました.
今回は以前の成果に加えて,CUDA
カーネルの高速化に取り組みました.
並列計算におけるデータの安全性を保つために不可欠な
atomicAdd 命令.
しかし,その安全性の代償として生じる重さが今回のボトルネックでした.
本記事では,この atomicAdd
の呼び出し回数を大幅に削減し,高速化を達成したアプローチを解説します.
3D Gaussian Splatting とは?
3D Gaussian Splatting for Real-Time Radiance Field Rendering とは,2023 年に提案された手法です. 新規ビュー合成(Novel-view Synthesis)のための訓練とレンダリング(描画)を高速,高精細に行うことができます. 新規ビュー合成とは,複数枚の画像から 3 次元形状を推定し,3 次元モデルを作成する手法です.
推定した 3 次元モデルを利用することにより,新たなビュー(画角)から撮影された画像をレンダリングします.

3D Gaussian Splatting では,3 次元モデルを以下の図のように,いくつかの 3D Gaussian の組み合わせで表現します.

これにより,高速な 3 次元形状推定とレンダリングを両立しています.
3D Gaussian とは,3D 共分散行列 \(\Sigma\) と中心となる点 \(\mathbf\mu\) を用いて,その形状が \(G(\mathbf x) = e^{-\frac{1}{2}(\mathbf x – \mathbf \mu)^\top\Sigma^{-1}(\mathbf x – \mathbf \mu)}\) で表されます.
この式は位置 \(\mathbf\mu\) と,広がり \(\Sigma\) を使って,ぼんやりとした色のついた塊(3D Gaussian)を定義しています. これを無数に集めて,1 つの 3D モデルを表現します.
3D Gaussian は形状の情報に加えて,色の情報,不透明度の情報を持ちます. これらのパラメータの最適化や,3D Gaussian の数を増減させることにより,より高精細な 3 次元モデルを作成します.
高速化へのアプローチ
プロファイリングによるボトルネックの発見
ここからは,より具体的な処理の流れと,高速化へのアプローチについて述べていきます.
3D Gaussian Splatting では,以下のプロセスを繰り返すことにより 3 次元モデルを最適化します.
- 画像の選択
入力画像のうち,1 枚を選択します. - レンダリング
選択した画像と同じ位置姿勢からレンダリングを行います. - 誤差の計算
レンダリングした画像と,元の画像の誤差を計算します.\(\mathcal{L}_1\) ノルムと SSIM を組み合わせた値を誤差として用います. - 勾配計算
それぞれの 3D Gaussian のパラメータについて,最終的な誤差に対する各パラメータの偏微分を計算します. - 更新
計算した偏微分の値を用いて,パラメータの更新や 3D Gaussian の増減を行います.
実際にプロファイリングを行ったところ,勾配計算がネックであり,全体の処理時間の約 55 % を勾配の計算が占めているということがわかりました. プロファイリングには NVIDIA Nsight Systems を用いました.
ボトルネックとなっている勾配の計算は,元の実装では CUDA C++ により書かれています. CUDA C++ とは,NVIDIA 社が開発した,C++ を拡張した GPU 向けのプログラミング言語です. GPU の性能を最大限発揮するために用いられます.
CPU と GPU
GPU とは Graphics Processing Unit の略で,その名の通り元々は画像処理を専門とする演算装置でした. その最大の強みは並列計算にあります. 並列計算とは,たくさんの計算を小分けにして,複数のコア(計算を担当する回路)で文字通り同時に処理を行う方法です. 1 つのコアが順番にタスクを処理する逐次処理と比較して,処理時間を大幅に短縮できる場合があります. この GPU の能力を画像処理以外にも応用する技術は GPGPU(General-Purpose computing on Graphics Processing Units)と呼ばれ,現在では様々な科学技術計算やシミュレーションなどに活用されています.
GPU が並列計算が得意である理由,それは CPU との構造的な違いにあります.
- CPU(Central Processing Unit)
数個から数十個の高性能なコアを持ち,各コアは複雑で逐次的な命令を高速に処理することに特化しています. OS や一般的なアプリケーションの実行など,様々なタスクに用いられる万能な演算装置です.
普段,コンピュータ上で多数のアプリケーションが同時に動いているように見えます. 実際に目に見えるアプリケーションだけでなく,見えないところでもたくさんの処理が走っています. これは,CPU が持つ複数のコアで別々の処理を同時に実行(並列処理)しつつ,さらに各コアが OS の制御のもと,担当する処理を人間が知覚できない速度で切り替え続けている(並行処理)ためです. これにより,コアの数よりも遥かに多くのタスクを,あたかも同時に動いているかのように見せかけています.
- GPU(Graphics Processing Unit)
数千個以上の比較的シンプルなコアを持ちます. 各コアの性能は CPU に劣りますが,その圧倒的な数により,同じ種類の単純な計算を大規模に一斉に実行することに特化しています.
近年,機械学習の分野で GPU が不可欠な存在となっているのは,この特性が理由です. 機械学習の計算の多くは,巨大な行列に対する単純な四則演算の繰り返しです. これは,GPU が最も得意とする同じ種類の単純な計算を大規模に行うタスクそのものです.
既に元の実装の時点で,CUDA を用いた並列化による高速化は行われていました. しかし,その処理内容を深く分析し,GPU の能力をより効率的に引き出すことによりさらなる高速化を目指しました.
GPU
を使った並列計算では,数千のコアがそれぞれ計算した結果を,最終的に 1
つの共有メモリに集計(合計)する必要があることがあります.
しかし,ここで単純な加算処理を複数のスレッドから同時に行うと,競合状態が発生し,その結果が正しく計算されない場合があります.
これは,加算処理が「メモリからの値の読み込み」,「値の変更」,「メモリへの値の書き込み」という複数のステップから構成されているためです.
例えば,共有メモリの値が 10 のときに,スレッド A が
1 を,スレッド B が 2
を加算しようとすると,以下のようにスレッド A
の計算結果が失われてしまうケースが起こりえます.
| 時刻 | スレッド A | スレッド B | メモリ |
|---|---|---|---|
| 0 | 10 | ||
| 1 | メモリから値 10 を読み込む | 10 | |
| 2 | メモリから値 10 を読み込む | 10 | |
| 3 | 読み込んだ 10 に 1 を加え,11 を計算 | 10 | |
| 4 | 読み込んだ 10 に 2 を加え,12 を計算 | 10 | |
| 5 | 計算結果 11 をメモリに書き込む | 11 | |
| 6 | 計算結果 12 をメモリに書き込む | 12 |
本来は結果として 13(10 + 1 + 2)となるべきところが,最終的にメモリに書き込まれた値は 12 となってしまい,スレッド A の計算した結果(+ 1)が失われています.
この問題を解決し,競合を起こさずに加算を行うための命令が
atomicAdd です. atomicAdd
は,一連の加算処理が他のスレッドから割り込まれないように保護(ロック)する仕組みです.
勾配計算の高速化
– atomicAdd の呼び出しの削減
atomicAdd
はデータの安全性を保証する強力な命令ですが,その仕組み上,通常の加算命令と比較して大きなオーバーヘッドが発生します.
そして,元の実装のネックとなっていたのが,この atomicAdd
が大量に呼び出されていたところでした.
そこで,atomicAdd
の呼び出し回数を減らすことで高速化を目指しました.
元の実装では,atomicAdd
を用いて,それぞれのスレッドで計算した勾配情報(偏微分の値)を集計していました.
そこで,1 つのスレッドの計算結果を atomicAdd
するのではなく,スレッドのまとまりであるブロック単位で集計したのちに,1
度だけ atomicAdd を行うように処理を変更しました.
元の実装では 1 ブロックあたり 256
スレッドで構成されていたため,ブロック内の処理をまとめることで,atomicAdd
の(スレッド数に対する)呼び出し回数を元の \(\frac{1}{256}\)
にまで削減することができました.
ブロック単位で値の和を集計するためには,リダクションと呼ばれる手法が効果的です. これを行うためには,ブロック内のスレッドがデータを共有するための共有メモリを中間結果の保存に利用する必要があります.
しかし,共有メモリは利用できる量が限られています. そのため,単純にリダクションを組み込むだけでは,メモリが不足したり,実行効率が下がるという事象が確認されました. そこで,この共有メモリの制約の中で効率を最大化するために,ブロックサイズの最適化を行いました. 具体的には,1 ブロック当たりのスレッド数を調節し,1 つのスレッドが計算を担当するピクセルの数を増加させました. これにより,共有メモリの使用量を最適な範囲に保ちつつ,メモリアクセスや同期のコストを削減し,GPU 全体の性能を最大限引き出しました.
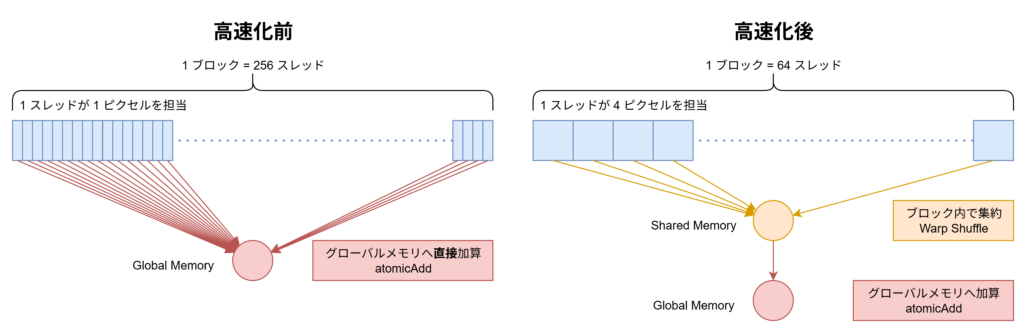
CUDA におけるリダクションの実装について
ブロック内リダクションは CUDA ではいくつかの実装方法があります.
代表的な方法が,ブロック内のスレッドが共有して使える高速な
shared memory を一時的なバッファとして用いる方法です.
また,__shfl_down_sync
のようなワープ内シャッフル命令を用いることで
shared memory
を介さずにスレッド間で直接データを交換しながら合計値を計算する方法も非常に高速です.
今回はこれらの手法を組み合わせ,効率的な集計処理を実装しました.
- ワープ:32 スレッドからなる GPU の同時実行単位
今回紹介した atomicAdd を削減する手法に加えて,以前の記事で行った高速化手法を加えました.
この高速化手法はSpeedy-Splat の AccuTile
という手法とアイデアが被ってしまっており,Speedy-Splat
の実装も参考にしつつ,前回の記事より高速な形で実装を行いました.
検証
3D Gaussian Splatting のオリジナル版と, その派生手法である EDGS についてそれぞれ今回の手法を実装し,比較を行いました.
データセットとして,Tank and Temples の Train を用いました.
以下,今回の atomicAdd を削減する手法を手法
A,以前の記事で行った高速化手法の改良版を手法 B と表記します. 手法 A
と手法 B は独立しており,片方だけを導入することが可能です.
今回は,何も加えなかった場合,手法 A のみを導入した場合と,手法 A と B 両方導入した場合の 3 つの条件について検証を行いました.
環境として,CPU は Intel Core i9-10900,GPU は NVIDIA GeForce RTX 5060 Ti を用いました. 学習は 30,000 ステップ行い,その時点での総実行時間を計測しました.
| 手法 | 実行時間(秒) | 元実装に対する実行時間(%) |
|---|---|---|
| オリジナル | 1,419 | 100 |
| オリジナル + 手法 A | 1,167 | 82 |
| オリジナル + 手法 A + 手法 B | 866 | 61 |
| EDGS | 2,136 | 100 |
| EDGS + 手法 A | 2,022 | 95 |
| EDGS + 手法 A + 手法 B | 1,837 | 86 |
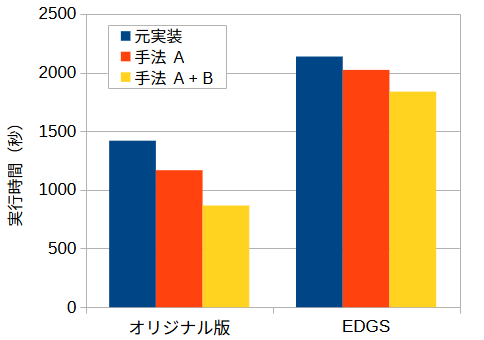
以上のように,今回の実装により,より高速な処理が可能となりました.
オリジナル版については約 40 %,EDGS についても約 15 % の実行時間を削減を達成しました.
オリジナル版と比較して EDGS の高速化が穏やかであった原因として, 両手法における 3D Gaussian の特性の違いが考えられます. EDGS は,より密で小さい 3D Gaussian を生成することで, 少ない学習ステップで高品質なモデルを構築する傾向があります. 今回の手法は比較的大きな 3D Gaussian が広範囲を覆うときに効果を発揮しやすく, また,オリジナル版をより高速にするようにパラメータを含めて調整したため, この差が生じたと考えられます. EDGS の特性に合わせたチューニングを施すことで,さらなる高速化が期待できます.
補足:EDGS の実行時間について
今回検証した EDGS の実行時間がオリジナル版を上回っていますが,これは学習ステップを 30,000 回に固定したためです.EDGS は,より少ないステップ数で高品質なレンダリング結果を得られる手法であり,「特定の品質に到達するまでの時間」で比較すれば,多くの場合で EDGS がオリジナル版を上回る性能を発揮することをご留意ください.
おわりに
今回実装した atomicAdd の削減手法は,勾配計算という 3D
Gaussian Splatting の根幹にかかわる処理を対象としています.
そのため,現在提案されている数多くの 3D Gaussian Splatting
の派生手法についても同様に組み込むことが可能であり,さらなる高速化を実現できると期待されます.
このような CUDA カーネルレベルでの根本的なボトルネックの解析と最適化は,Fixstars が最も得意とする分野のひとつです. Fixstars では,インターンシップや新卒・中途採用を通じて,計算の高速化に情熱を注ぐ仲間を募集しています. 今回の記事で紹介したような技術に挑戦してみたい方は,ぜひ採用ページをご確認ください.
Tags
Leave a Comment
Tags
Archives
- 2026年2月
- 2026年1月
- 2025年12月
- 2025年11月
- 2025年8月
- 2025年5月
- 2025年4月
- 2024年11月
- 2024年10月
- 2024年7月
- 2024年5月
- 2024年4月
- 2024年2月
- 2024年1月
- 2023年12月
- 2023年6月
- 2023年5月
- 2023年4月
- 2023年2月
- 2023年1月
- 2022年12月
- 2022年10月
- 2021年11月
- 2021年9月
- 2021年6月
- 2021年3月
- 2021年2月
- 2020年12月
- 2020年10月
- 2020年7月
- 2020年6月
- 2020年5月
- 2020年4月
- 2020年3月
- 2020年2月
- 2020年1月
- 2019年12月
- 2019年11月
- 2019年10月
- 2019年9月
- 2019年8月
- 2019年6月
- 2019年4月
- 2019年3月
- 2019年2月
- 2019年1月
- 2018年12月
- 2018年11月
- 2018年10月
- 2018年8月
- 2018年6月
- 2018年5月
- 2018年4月
- 2018年3月
- 2018年2月
- 2017年12月
- 2017年11月
- 2017年10月
- 2017年9月
- 2017年8月
- 2017年7月
- 2017年6月
- 2017年5月
- 2017年3月
- 2016年12月
- 2016年11月
- 2016年8月
- 2016年7月
- 2016年3月
- 2016年2月
- 2016年1月
- 2015年12月
- 2015年11月
- 2015年10月
- 2015年8月
- 2015年6月
- 2015年3月
- 2015年2月
- 2015年1月
- 2014年12月
- 2014年11月



keisuke.kimura in Livox Mid-360をROS1/ROS2で動かしてみた
Sorry for the delay in replying. I have done SLAM (FAST_LIO) with Livox MID360, but for various reasons I have not be...
Miya in ウエハースケールエンジン向けSimulated Annealingを複数タイルによる並列化で実装しました
作成されたプロファイラがとても良さそうです :) ぜひ詳細を書いていただきたいです!...
Deivaprakash in Livox Mid-360をROS1/ROS2で動かしてみた
Hey guys myself deiva from India currently i am working in this Livox MID360 and eager to knwo whether you have done the...
岩崎システム設計 岩崎 満 in Alveo U50で10G Ethernetを試してみる
仕事の都合で、検索を行い、御社サイトにたどりつきました。 内容は大変参考になりま�...
Prabuddhi Wariyapperuma in Livox Mid-360をROS1/ROS2で動かしてみた
This issue was sorted....