整数型 と Newton法

メモリ事業部の 眞鍋 です。

本日は 「整数型 と Newton 法」という話題を取り上げたいと思います。

Newton 法 はその意味から察するに もともと実数など を対象にした技法なのですが、

整数型でも意味がつくんだ！ ということを紹介するのが今回のテーマであります。

整数型 Newton 法の例として、 除算の例・5次方程式の例を取り上げたいと思います。

まずはその前に以前の記事の復習から始めたいと思います。

以前記載の記事について

以前紹介した記事「2の補数表現をちょっと違った見方をしてみる」では

次のような問いかけを主テーマに行いました：

上の内容を数遊びを通じて、スマートに示せたと思っております。

今回のお話も「天までつづく数の世界」でできることを、

似ているはずの整数型にも持ち込んでみる、という背景になります。

そして前回の記事の最後で、次のような紹介をしました：

$x / (-15) $ を計算する際、

$(-15)  a = 1$  を満たす $a$ を見つけました。つまり $ \displaystyle a = -\frac{1}{15}$ に相当する 整数 を見つけました。

具体的には uint32_t の世界では

$$ a = 1 + 16 + 16^2 + 16^3 + ・・・  16^7$$

でした。

そして $x / (-15)$ という 除算演算 を

$x \times a$ という 乗算 に帰着させる話を持ち出しました。

そのことを確認するために

$(-15)/(-15) = 1$ が $(-15) \times a$ で置き換えられることも見ました：

この例は簡単に

幾何級数：

$$1/(1-x) = 1 + x + x^2 + x^3 + x^4 + ・・・$$

を応用するための式でありました。

そのため 非常に限定的な最適化の話 である

$x / (-15)$ という式で、なおかつ $x$ が 15 の倍数というシチュエーションにこの置き換えができる

という紹介をしました。

そんな例、正直、そうそうないよ…という気持ちで

読まれた方が多かったのではないかと思います。

ただ、「天までつづく数の世界」とのつながり を説明する、という点ではわかりやすい記事だったと思います。

以上が 「2の補数表現をちょっと違った見方をしてみる」の、今回のお話とつながる点の復習でした。

今回の記事の目的

今回はもう少し意味のある例を考えてみたいと思います。

上では  $(-15)  a = 1$ となる $a$ を見つけることができたわけですが

例えば $7 a = 1$ となるような $a$ は見つけることができるでしょうか。

自分は、上の幾何級数をつかって見つけることができませんでした。

この記事では具体的に 7 の場合を挙げますが他の場合も同様にできますので

この具体例で進めたいと思います。

注. $2 a = 1$ などの式は明らかに解を持ちませんので解がある場合で応用してください。

Newton 法の登場

Newton 法をご存知でしょうか？

関数 $f$ が与えられた時に $f(x) = 0 $となる $\alpha$ を近似する技法の一つです。

下の図のように $x_n$ について接線を引いて

$x$ 座標とのぶつかったところを新たに $x_{n+1}$ とします。

これを延々と繰り返しますと $x_n$ が $\alpha$ に収束する気がします。

注. 記事が長くなりすぎたため、収束証明・収束オーダーの話は割愛させていただきます。

式で記すと次のような式になります:
$$ \displaystyle x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)} $$

このイメージ図を考えると

「整数型」について Newton 法が使えないのでは？ という気持ちになります。

なぜなら整数というのは $\dotsc, -2, -1, 0, 1, 2, \dotsc $ という離散的なものなので

上のような滑らかなグラフは描けないからです。

今回の記事の主目的は、

「整数世界でも Newton 法が なぜか 役に立つんだ」

という新しい目線を紹介できればと思っております。

こうした視点は何の役に立つのでしょうか？

「ハッカーのたのしみ」と呼ばれる本には 整数型平方根 の高速化話題が登場します。

その話のバックグラウンドには、実はこの話題と関係があるのです。

ということで役立つテクニックなのです。

Newton 法を適用してみる — 失敗編 —

今回考える例は $ 7x = 1$ なる $x$ を求めることでした。

つまり $7x – 1 = 0$ を求めたいので

$f(x) = 7x – 1$ とやりたいのですが

実はこれはうまくいきません。

$$ \displaystyle x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)} = x_n – \frac{7x_n-1}{7} = \frac{1}{7} $$

という式になり $x_{n}$ が消えて意味のない式になってしまいます。

Newton 法を適用してみる — 成功編 —

ここでは $7x-1=0$ を式変形した

$$\displaystyle \frac{1}{x} – 7 = 0$$

で考えることにしてみます。

そこで $$\displaystyle f(x) = \frac{1}{x} – 7$$ として先ほどの Newton 法の式を持ち出します。

すると

$$ \displaystyle x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)} = x_n – \frac{ \frac{1}{x_n} – 7   }{ -\frac{1}{{x_n}^2} } =  2x_n – 7x_n^2$$

となります。

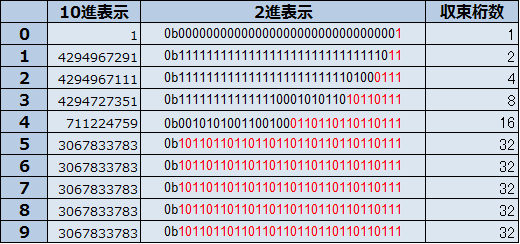
この式を利用して $x_0 = 1$ から計算しますと次のようになります：

何やらある値に収束しました。

この値と例えば $42$ の掛け算を行うと

このように $6$ になります。

そのため $1/7$ の役割をもった数字を得ることができたことがわかります。

このことから、

$x / 7$ を $x \times 3067833783$ で置き換えることができそうです。

この除算方法の注意・応用方法

この除算高速化は $ x / a $ を高速化するのに使えると言えるのでしょうか？

実は微妙なところであります。

例えば $x$ が 7 の倍数でないのに

$x / 7$ を $x \times 3067833783$ で置き換えると大変なことになります。

例えば $x = 1$ のときは $3067833783$ になってしまいます。

つまり 先ほどの例は $x$ が 7の倍数 でしか使えないとも言えます。

しかし、別の視点をもつと意味があります。

$ (((3 / 7) \times 2 )\times 7)  $ を $(( 0 \times 2 )\times 7)$ と評価したい場合と、

分数として計算して $6$ と評価してほしい場合があります。

この場合 $6$ となることを期待している場合には

$ (((3 \times 3067833783) \times 2 )\times 7) $ として uint32_t で計算すると $6$ になり

置き換えができます。有理数的な観点で応用できる技法と言えそうです。

ただ 普通の整数除算の立場 からみると、すごく役に立たなさそうに見えます。

実は いわゆる $ x / 7 $ を乗算などで最適化する方法は他の方法で知られています。

残念ながら今回はこの方法がメインテーマでないため、紹介しません。

紹介する機会がありましたら説明したいと思います。

この除算テクニックの真なる応用は、例えば次のようなものがあります：

整数型と5次方程式

続いて

$$x^5 + 2x^4 + 3x^3 + 4x^2 + 5x + 6 = 0$$

という 5次方程式 を考えてみたいと思います。

非常に適当につくった5次方程式です。

一般的に5次以上の方程式は解の公式がないことが知られています。

実際 Maxima などの計算ソフトでは上の厳密解を求めることができませんでした。

しかしながら 整数型の世界 ではどうでしょう？

$$ f(x) = x^5 + 2x^4 + 3x^3 + 4x^2 + 5x + 6 $$ として

Newton 法にかけてみます：

$$ x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)} =
x_n – \frac{x_n^5 + 2x_n^4 + 3x_n^3 + 4x_n^2 + 5x_n + 6}{5x_n^4+8x_n^3+9x_n^2+8x_n+5 } $$

という式になります。

ここで

$$ \frac{1}{5x_n^4+8x_n^3+9x_n^2+8x_n+5} $$

という式が登場していますが

この計算は上でやった $ax = 1$ を求める方法で計算できるわけです。

これを先ほどの方法でなく、いわゆる C言語の 整数型割り算の挙動 で実施してしまうと収束しません。

例えば $x_0 = 1$ から始めると

$$ x_1 = x_0 – \frac{x_0^5 + 2x_0^4 + 3x_0^3 + 4x_0^2 + 5x_0 + 6}{5x_0^4+8x_0^3+9x_0^2+8x_0+5 } =  1 – \frac{1 + 2 + 3 + 4 + 5 + 6}{5+8+9+8+5 } =  1 – \frac{21}{35 } $$

となり C言語の整数型割り算では $21/35 = 0$ なので ずっと $1$ になってしまいます。

そのため、今まで準備してきた方法が活きます。

$ax = 1$ を求める方法で計算するとこの計算はきちんと続き、 $x_0 = 1$ から始めると

となります。
さてここで求めた値をいれますときちんともとの方程式を満たすことが確認できます。

つまり uint32_t において 5次方程式の厳密解を見つけることができました。

ここまでのまとめ

数学的な証明などを説明せず、フィーリング数学で進めてしまいましたがいかがでしょうか。

次のようなことを説明しました：

• 実数用の Newton 法が そのままの式で 整数型でも役立つ例を紹介した
• この技を使って、除算を乗算に置き換える技は超特殊な場合使えそう
• 「ハッカーのたのしみ」と呼ばれる本の 整数型平方根・整数立方根 の高速化技法で、なぜ Newton 法の式が整数型でもでてくるのかの理由が少し見えてきた
• この技法は多項式全般で応用が効きそうなことが紹介できた

以上です。

This site uses Akismet to reduce spam. Learn how your comment data is processed.