「DualSPHysicsで静水圧問題」を発表してきました

アルバイトの大友です．
2019年6月にフィックスターズで開催されました第76会オープンCAE勉強会@関東（流体など）【大崎】で「DualSPHysicsで静⽔圧問題」（大友広幸，吉藤尚生）と題して発表をしてきました．

発表内容

フィックスターズはOpenMPSというMPS法（粒子法の一種）を用いた数値流体ソルバーの開発に参加しています．
私は昨年よりOpenMPSとの比較対象としてDualSPHysicsというSPH法（同じく粒子法の一種）を用いたFLOSSの流体シミュレータの調査を行っています．
その過程でDualSPHysicsでは静水圧問題が正しく解けていないことを発見し，その原因の調査結果を発表しました．

静水圧問題

ざっくり言うとコップに水を入れて放置する問題です．
期待される結果は放置前と放置後で水位などが変わらないことです．
しかしDualSPHysicsでは水位が上昇します．

原因の調査

静水圧問題で水位が上昇する問題を調査するにあたって，壁面境界を除去し問題を単純化するために中心重力問題を用いました．
中心重力問題ではすべての粒子は空間のある点（中心）に向かって一定の力がかかります．
万有引力のように中心からの距離に応じて力の大きさが変わることはありません．
式で書くと
$$
\mathbf{F}_i = -m_i g\frac{\mathbf{r}_i-\mathbf{r}_{\mathrm{center}}}{|\mathbf{r}_i-\mathbf{r}_{\mathrm{center}}|}
$$
となります（$\mathbf{F}_i$:粒子$i$に対する中心重力，$g$:重力加速度，$\mathbf{r}_i$:粒子$i$の位置，$\mathbf{r}_{\mathrm{center}}$:中心の位置）．
中心重力問題では十分時間が経つと円盤に収束することが期待されます．
実際にOpenMPSでは円盤に収束することが確認されています[中心重力による静水圧問題の妥当性確認 – OpenMps]．

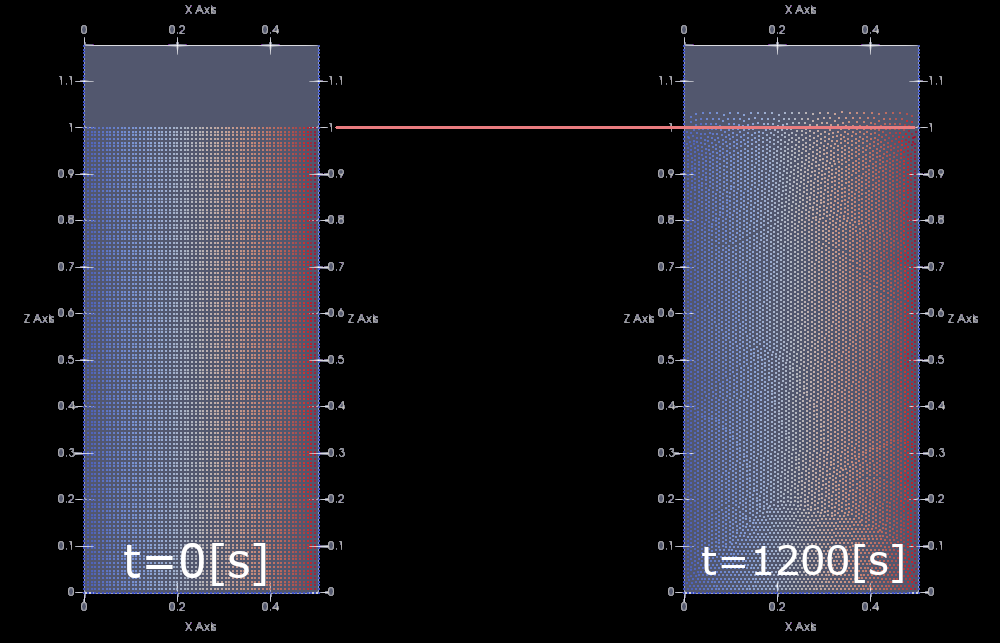
DualSPHysicsで中心重力問題を解くと下図のように中心付近が密，中心から離れるにつれ疎となっていきました．
これはコップでの静水圧問題の問題点が中心重力問題でも現れているということになります．

DualSPHysicsによる中心重力問題

DualSPHysicsのソースコードをいじるのは大変だったので，自分でWCSPH（Weakly Compressible SPH）のシミュレータを実装し，DualSPHysicsと同じ問題が起こるかを調査しました．
その結果，自分で実装したシミュレータではこの問題は起こりませんでした．

密度計算が怪しい

自分の実装では粒子$i$の密度$\rho_i$を
$$
\rho_i = \sum_j m_j W_{ij}
$$
と計算していました（$m_j$:粒子$j$の質量，$W_{ij}$:カーネル関数）．
こちらを以降「カーネル和による密度計算」と呼びます．

一方DualSPHysicsでは
$$
\frac{D\rho_j}{Dt} = – \sum_j m_j (\mathbf{u}_j – \mathbf{u}_i) \cdot \nabla \mathbf{W}_{i,j}
$$
と，密度の時間微分を計算し，時間発展させる形で密度を計算しています（$\mathbf{u}_j$:粒子$i$の速度）．
こちらを以降「時間発展による密度計算」と呼びます．

なんとなくこの密度計算が怪しそうだったので，自分の実装でも時間発展による密度計算でシミュレーションを行いました．

シミュレーション結果

シミュレーション結果を評価するため，

• 真円率（円盤らしさ）
• 半径

を計算しました．

カーネル和による密度計算の場合

真円率

時間がたつに連れ円盤に収束していっているのがわかります．

半径

• 半径（$R/r$: 自由表面と判定された粒子の中心からの距離の最大値/最小値）
  
• 半径変化
  

今回の問題設定では収束半径の理論値が$$\sqrt{\frac{4}{\pi}}\sim 1.128$$なので若干小さくなっている気はしますが，半径変化も0となり収束していると言えます．

時間発展による密度計算の場合

明らかに大きくなっています．

真円率

時間が経つと自由表面がデコボコして真円率が下がっているようです．

半径

• 半径（$R/r$: 自由表面と判定された粒子の中心からの距離の最大値/最小値）
  
• 半径変化
  

比較的時間が経っていない場合でも半径は大きくなっていき，600秒を過ぎたあたりで大きく増加しているのがわかります．

結論

DualSPHysicsで静水圧問題が解けない問題は時間発展型の密度計算が関わっていそうです．

今後の調査方針（今やっていること）

• DualSPHysicsでカーネル和による密度計算を行い，静水圧問題が解けるようになるかを調べる．
• 時間発展による密度計算で静水圧問題が解けないのであればそれを理論的に解明し，修正が可能か検討する．

参考文献

1. 後藤仁志 粒子法 森北出版 2018

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。