ディリクレ過程混合モデルによるクラスタリング（実践導入編）

前回の続きから

前回、前々回でディリクレ過程混合モデルによるクラスタリングの手法について見てみました。今回は、実際にデータを使ってクラスタリングしてみたいと思います。前回の最後にクラスタリングの具体的手順を記載したのですが、具体的と言いつつコードに落とし込めるレベルにはなっていなかったので、今回はコーディングできるレベルでの手順を示したいと思います。
実データで実験を行うためには、$G_0$ の形を具体的に決める必要があります。$G_0$ はクラスタパラメータ $\boldsymbol{\theta}$ を生成する確率密度関数です。クラスタに所属するデータは正規分布に従うものとしましょう。そうすると、クラスタパラメータは正規分布の平均 $\boldsymbol{\mu}$ と共分散 $\Sigma$ になります。クラスタデータは正規分布 $N(\boldsymbol{x}; \mu, \Sigma)$ に従うとするわけです。さて、正規分布のパラメータ $\boldsymbol{\theta} = (\boldsymbol{\mu}, \Sigma)$ が従う $G_0$ は、どのような確率分布になるのでしょうか？
ギブスサンプリングによってデータを生成する場合、そのデータがどのクラスタに所属するか、確率的に決定する必要があります。クラスタ 1 に所属するのか、クラスタ c に所属するのか、それとも新しいクラスタに所属するのか、それぞれの確率を計算する必要があります。これらのうち、新しいクラスタに所属する場合の確率計算には、$G_0$ の積分が登場します。
新規クラスタを生成する確率は、以下です。$$P_{new} ∝ \frac{\alpha}{n – 1 + \alpha} \int p(\boldsymbol{x}_i|\boldsymbol{\theta})G_0(\boldsymbol{\theta})d\boldsymbol{\theta}$$
積分の中をよく見ると、これはベイズの定理で言うところの「尤度」x「事前確率」となっているようです。

$p(\boldsymbol{x}_i|\boldsymbol{\theta})$ ⇒ $\theta$ が与えられた状態で得られたデータ $\boldsymbol{x}$ の尤度

$G_0(\boldsymbol{\theta})$ ⇒　$\boldsymbol{\theta}$ の事前確率

「$\boldsymbol{\theta}$ の事後確率」∝「$\boldsymbol{\theta}$ が与えらえている状況での $\boldsymbol{x}$ の尤度」x「$\boldsymbol{\theta}$ の事前確率」なので、求めたい積分 ∝「$\boldsymbol{\theta}$ の事後確率」の積分です。この場合、事前確率と事後確率が同じ確率分布になっているとよいことがあります。これはつまり、事前分布が共役事前分布だとよいと言っているわけですが、なぜよいかというと、この積分が解析的に解けてしまうからです。
共役事前分布でない場合を考えてみましょう。

$$p(\boldsymbol{x} | \boldsymbol{\theta})p(\boldsymbol{\theta}) = p(\boldsymbol{\theta} | \boldsymbol{x})p(\boldsymbol{x})$$

一般的に成立するこの式の両辺を $\boldsymbol{\theta}$ で積分してみましょう。

$$\int p(\boldsymbol{x} | \boldsymbol{\theta})p(\boldsymbol{\theta})d\boldsymbol{\theta} = \int p(\boldsymbol{\theta} | \boldsymbol{x})p(\boldsymbol{x})d\boldsymbol{\theta}$$

右辺 $= p(\boldsymbol{x})\int p(\boldsymbol{\theta} | \boldsymbol{x})d\boldsymbol{\theta} = p(\boldsymbol{x})$ となるので、

$$\int p(\boldsymbol{x} | \boldsymbol{\theta})p(\boldsymbol{\theta})d\boldsymbol{\theta} = p(\boldsymbol{x})$$

となります。左辺の積分は定数となることは分かりますが（当たり前だ！）、それ以上のことは分かりません。ここで、事前確率 $p(\boldsymbol{\theta})$ と事後確率 $p(\boldsymbol{\theta} | \boldsymbol{x})$ が同じ関数形で書けるとしたらどうでしょう？

$$p(\boldsymbol{x} | \boldsymbol{\theta})G(\boldsymbol{\theta}; \boldsymbol{\nu}) = C(\boldsymbol{x}, \boldsymbol{\nu})G(\boldsymbol{\theta}; \boldsymbol{\nu’})$$

ここで、$G(\boldsymbol{\theta}; \boldsymbol{\nu})$ と $G(\boldsymbol{\theta}; \boldsymbol{\nu’})$ は関数形は同じでパラメータだけ異なることを表現しています。事前分布と事後分布は同じ関数形に書け、また定数倍が許されます。その定数は、サンプルデータ $\boldsymbol{x}$ と事前分布のパラメータ $\boldsymbol{\nu}$ の関数になっているはずです。事後分布のパラメータ $\boldsymbol{\nu’}$ と定数 $C(\boldsymbol{x}, \boldsymbol{\nu})$ は解析的に求められるものとします。解析的に求められるものでなければ、それは共役事前分布とは言えません。この両辺を $\boldsymbol{\theta}$ で積分すると、

$$\int p(\boldsymbol{x} | \boldsymbol{\theta})G(\boldsymbol{\theta})d\boldsymbol{\theta} = C(\boldsymbol{x}, \boldsymbol{\nu})$$

となり、積分は解析的に求められる定数となります。というわけで、事前分布として $\boldsymbol{\theta}$ の共役事前分布を選ぶとよいのです！

ウィシャート分布

今、$\boldsymbol{\theta}$ は何かというとクラスタのパラメータなわけで、具体的には正規分布の $\boldsymbol{\mu}$ と共分散 $\Sigma$ にすると決めました。ただ、これ以降は $\Sigma$ の代わりに $\Lambda = \Sigma^{-1}$ をパラメータとして扱います。つまり、$\boldsymbol{\theta} = (\boldsymbol{\mu}, \Lambda)$ です。
正規分布のパラメータ $\boldsymbol{\theta} = (\boldsymbol{\mu}, \Lambda)$ の共役事前分布は何になるかというと、正規ウィシャート分布という分布です。正規ウィシャート分布を表す関数は、正規分布関数とウィシャート分布関数の積です。

正規分布のパラメータは $(\boldsymbol{\mu}, \Lambda)$ です。ここからデータ $\boldsymbol{x}$ が生成されるとすると、$\boldsymbol{x}$ の生成確率は以下の式に従います。

$$N(\boldsymbol{x}; \boldsymbol{\mu}, \Lambda^{-1}) = \frac{|\boldsymbol{\Lambda}|^\frac{1}{2}}{2\pi^\frac{d}{2}}exp[-\frac{1}{2}(\boldsymbol{x} – \boldsymbol{\mu})^t\boldsymbol{\Lambda}(\boldsymbol{x} – \boldsymbol{\mu})]$$

ウィシャート分布のパラメータは $(\nu, S)$ です。$\nu$ はスカラー値、$S$ は正方行列です。ここからデータ $X$ が生成されるとすると ($X$ も正方行列)、$X$ の生成確率は以下の式に従います。

$$W(X; \nu, S) = \frac{|X|^{(\nu-d-1)/2}exp[-\frac{1}{2}tr(S^{-1}X)]}{2^{{\nu}d/2}\pi^{d(d-1)/4}|S|^{\nu/2}\prod_{j=1}^d\Gamma(\frac{\nu+1-j}{2})}$$

$\Gamma$ 関数が出てきましたが、これは階乗みたいな値を返す関数です。また、$d$ はデータの次元数です。

クラスタパラメータ $\boldsymbol{\theta} = (\boldsymbol{\mu}, \Lambda)$ の生成確率は、以下の正規ウィシャート分布の式に従います。

$$N(\boldsymbol{\mu}; \boldsymbol{\mu}_0, (\beta\Lambda)^{-1})W(\Lambda; \nu, S)$$

即ち、

$$G_0(\boldsymbol{\theta}) = G_0(\boldsymbol{\mu}, \Lambda) = N(\boldsymbol{\mu}; \boldsymbol{\mu}_0, (\beta\Lambda)^{-1})W(\Lambda; \nu, S)$$

となります。$\Lambda$ の出やすさを制御するのがウィシャート分布のパラメータ $\nu, S$ であり、$\boldsymbol{\mu}$ の出やすさを制御するのが $\boldsymbol{\mu}_0, \beta$, およびウィシャート分布から生成された $\Lambda$ です。ややこしいですね。$\boldsymbol{\mu}_0, \beta, \nu, S$ は事前に値を割り当てなければならない定数であり、何らかの値を指定してやる必要があります。$\Lambda$ に関しては $S$ が $\Lambda$ の形を制御し、$\nu$ がばらつきやすさを制御していると思います。$\boldsymbol{\mu}$ に関しては、$\boldsymbol{\mu}_0$ が $\boldsymbol{\mu}$ の形を制御し、$\beta$ がばらつきやすさを制御していると思います。正規分布 $N(\boldsymbol{\mu}; \boldsymbol{\mu}_0, (\beta\Lambda)^{-1})$ に従って生成される $\boldsymbol{\mu}$ の平均は $\boldsymbol{\mu}_0$ ですが、ウィシャート分布 $W(\Lambda; \nu, S)$ に従って生成される $\Lambda$ の平均は ${\nu}S$ になります。

さて、$G_0(\boldsymbol{\theta})$ は共役事前分布なので、事後分布も同じ関数形に書けます。即ち、正規ウィシャート分布として書けます。実際に見てみましょう。尤度 × 事前分布の式から地道に変形していくと事後分布の式に辿り着くのですが、ここでは結果だけ書きます。

$$\begin{align}p(\boldsymbol{x} | \boldsymbol{\theta})G_0(\boldsymbol{\theta}) &= p(\boldsymbol{x} | \boldsymbol{\theta})N(\boldsymbol{\mu}; \boldsymbol{\mu}_0, (\beta\Lambda)^{-1})W(\Lambda; \nu, S) \\
&= N(\boldsymbol{x}; \boldsymbol{\mu}, \Lambda^{-1})N(\boldsymbol{\mu}; \boldsymbol{\mu}_0, (\beta\Lambda)^{-1})W(\Lambda; \nu, S) \\
&= (\frac{\beta}{(1 + \beta)\pi})^{d/2}\frac{|S_b|^{(\nu+1)/2}\Gamma(\frac{\nu+1}{2})}{|S|^{\nu/2}\Gamma(\frac{\nu + 1 – d}{2})}N(\boldsymbol{\mu}; \boldsymbol{\mu}_a, \Lambda_a^{-1})W(\Lambda; \nu + 1, S_b)\end{align}$$
ただし、
$$\boldsymbol{\mu}_a = \frac{\boldsymbol{x} + \beta\boldsymbol{\mu}_0}{1 + \beta} \\
\Lambda_a = (1 + \beta)\Lambda \\
S_b^{-1} = S^{-1} + \frac{\beta}{1 + \beta}(\boldsymbol{x} – \boldsymbol{\mu}_0)(\boldsymbol{x} – \boldsymbol{\mu}_0)^t$$
です。

両辺を $\boldsymbol{\theta}$ で積分すると、

$$\int p(\boldsymbol{x} | \boldsymbol{\theta})G_0(\boldsymbol{\theta})d\boldsymbol{\theta} = (\frac{\beta}{(1 + \beta)\pi})^{d/2}\frac{|S_b|^{(\nu+1)/2}\Gamma(\frac{\nu+1}{2})}{|S|^{\nu/2}\Gamma(\frac{\nu + 1 – d}{2})}$$

となります。この計算結果はギブスサンプリングの中で使います。
もう一つ解析解を求めておきます。クラスタに所属するサンプルデータが与えられた時、クラスタのパラメータを最尤推定するためです。ギブスサンプリングにおいて、クラスタの所属データが増減しますが、その都度パラメータを更新します。そのために必要な計算です。
クラスタ $i$ に $n_i$ 個のデータ $\boldsymbol{x}_{i1}, \boldsymbol{x}_{i2},…, \boldsymbol{x}_{in_i}$ が所属しているケースを考えます。$\boldsymbol{x}_{i1}, \boldsymbol{x}_{i2},…, \boldsymbol{x}_{in_i}$ が与えられている場合の $\boldsymbol{\theta}_i$ の事後確率 $p(\boldsymbol{\theta}_i | \boldsymbol{x}_{i1}, \boldsymbol{x}_{i2},…, \boldsymbol{x}_{in_i})$ を求めます。

$$\begin{align}p(\boldsymbol{\theta}_i | \boldsymbol{x}_{i1}, \boldsymbol{x}_{i2},…, \boldsymbol{x}_{in_i}) &= \frac{p(\boldsymbol{x}_{i1}, \boldsymbol{x}_{i2},…, \boldsymbol{x}_{in_i} | \boldsymbol{\theta}_i)G_0(\boldsymbol{\theta}_i)}{p(\boldsymbol{x}_{i1}, \boldsymbol{x}_{i2},…, \boldsymbol{x}_{in_i})} \\
&= \frac{p(\boldsymbol{x}_{i1}, \boldsymbol{x}_{i2},…, \boldsymbol{x}_{in_i} | \boldsymbol{\theta}_i)G_0(\boldsymbol{\theta}_i)}{\int p(\boldsymbol{x}_{i1}, \boldsymbol{x}_{i2},…, \boldsymbol{x}_{in_i} | \boldsymbol{\theta}_i)G_0(\boldsymbol{\theta}_i)d\boldsymbol{\theta}_i} \\
&= \frac{p(\boldsymbol{x}_{i1} | \boldsymbol{\theta}_i)p(\boldsymbol{x}_{i2} | \boldsymbol{\theta}_i)…p(\boldsymbol{x}_{in_i} | \boldsymbol{\theta}_i)G_0(\boldsymbol{\theta}_i)}{\int p(\boldsymbol{x}_{i1} | \boldsymbol{\theta}_i)p(\boldsymbol{x}_{i2} | \boldsymbol{\theta}_i)…p(\boldsymbol{x}_{in_i} | \boldsymbol{\theta}_i)G_0(\boldsymbol{\theta}_i)d\boldsymbol{\theta}_i}\end{align}$$

ここで、最右辺に $p(\boldsymbol{x}_{ij}|\boldsymbol{\theta_i}) = N(\boldsymbol{x}_{ij}; \boldsymbol{\nu}_i, \Lambda_i)\,(j = 1, 2,…, n_i),\,G_0(\boldsymbol{\theta}_i) = N(\boldsymbol{\mu}_i; \boldsymbol{\mu}_0, (\beta\Lambda_i)^{-1})W(\Lambda_i; \nu, S)$ を代入して頑張って計算していくと、以下を得ます。

$$p(\boldsymbol{\theta}_i | \boldsymbol{x}_{i1}, \boldsymbol{x}_{i2},…, \boldsymbol{x}_{in_i}) = N(\boldsymbol{\mu}_i; \boldsymbol{\mu}_c, \Lambda_c^{-1})W(\Lambda_i; \nu_c, S_q)$$
ただし、
$$S_q^{-1} = S^{-1} + \sum_{\boldsymbol{x}_k \in cluster-i} (\boldsymbol{x}_k – \bar{\boldsymbol{x}})(\boldsymbol{x}_k – \bar{\boldsymbol{x}})^t + \frac{n_{i}\beta}{n_i + \beta}(\bar{\boldsymbol{x}} – \boldsymbol{\mu}_0)(\bar{\boldsymbol{x}} – \boldsymbol{\mu}_0)^t \\
\bar{\boldsymbol{x}} = \frac{1}{n_i}\sum_{\boldsymbol{x}_k \in cluster-i}\boldsymbol{x}_k \\
\boldsymbol{\mu}_c = \frac{n_{i}\bar{\boldsymbol{x}} + \beta\boldsymbol{\mu}_0}{n_i + \beta} \\
\Lambda_c = (n_i + \beta)\Lambda_i \\
\nu_c = \nu + n_i$$
です。
$p(\boldsymbol{\theta}_i | \boldsymbol{x}_{i1}, \boldsymbol{x}_{i2},…, \boldsymbol{x}_{in_i}) = N(\boldsymbol{\mu}_i; \boldsymbol{\mu}_c, \Lambda_c^{-1})W(\Lambda_i; \nu_c, S_q)$ と正規ウィシャート分布になるわけですが、それでは一番出やすい $\boldsymbol{\mu}_i, \Lambda_i$ は何になるでしょうか？$N(\boldsymbol{\mu}; \boldsymbol{\mu}_0, \Lambda^{-1})$ に従う $\boldsymbol{\mu}$ の平均が $\boldsymbol{\mu}_0$ であること、$W(\Lambda; \nu, S)$ に従う $\Lambda$ の平均が ${\nu}S$ であることを考えると、$(\boldsymbol{\mu}_i, \Lambda_i)$ の最尤推定値は $(\boldsymbol{\mu}_c, {\nu_c}S_q)$ としてしまってよいと思います。ひょっとしたら厳密ではないかもしれませんが、今回の実験ではこうしました。クラスタに所属するデータが増減するたびに $\bar{\boldsymbol{x}}, n_i$ が変化しますが、その都度上式に従って $\boldsymbol{\mu}_c, {\nu_c}, S_q$ を計算して、${\boldsymbol{\theta}_i}$ の最尤推定値 $(\boldsymbol{\mu}_c, {\nu_c}S_q)$ を更新することになります。

ギブスサンプリング手順詳細

$G_0$ を正規ウィシャート分布 $N(\boldsymbol{\mu}; \boldsymbol{\mu}_0, (\beta\Lambda)^{-1})W(\Lambda; \nu, S)$ とする場合の手順詳細を示します。

1. 与えられたデータ $\boldsymbol{x} (= \boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n)$ を適当なクラスタに分割して $\boldsymbol{\theta} (= \boldsymbol{\theta}_1, \boldsymbol{\theta}_2, …, \boldsymbol{\theta}_c), \boldsymbol{s} (= s_1, s_2, …, s_n)$ の初期値を決めます。それぞれ別々の $n$ 個のクラスタに所属すると考えても OK です。その場合は、$s_k$ の初期値は $s_1 = 1, s_2 = 2, … s_n = n$ というようになり、クラスタ数 $c$ は $n$ になります。すべてのデータが 1つのクラスタに所属するとしても構いません。その場合は、$s_k$ の初期値はすべて 1 になり、クラスタ数 $c$ は $1$ になります。各クラスタのパラメータ $\boldsymbol{\theta}_i$ に関しては、いずれのケースでも $(\boldsymbol{\mu}_i, \Lambda_i) = (\boldsymbol{\mu}_c, {\nu_c}S_q)$ とします。
2. $s_k$ のいずれか一つをランダムに抜きます。$s_k$ を抜くと同時に $\boldsymbol{x}_k$ も抜きます。$\boldsymbol{x}_k$ を抜かれたクラスタに対しては、パラメータの最尤推定値を更新します。
3. $p(s_k|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x}) ∝ p(\boldsymbol{x}_i|\boldsymbol{\theta}_{s_k}) p(s_k|\boldsymbol{s}_{-k})$に基づき、$s_k$ を確率的に生成します。確率的に生成するとは、$p(s_k=1|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x}),\,p(s_k=2|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x}),\,…,\,p(s_k=c|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x}), p(s_k=new|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x})$ がそれぞれ計算できるので、例えば 0 – 1 の一様乱数を生成して、得られた値 $r$ が $0 \leq r < p(s_k=1|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x})$ ならば $s_k = 1$ とし、$p(s_k=1|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x}) \leq r < p(s_k=1|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x}) + p(s_k=2|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x})$ ならば $s_k = 2$, … とすれば OK です。$s_k$ が既存クラスタ $i$ に所属することになれば、$\boldsymbol{x}_k$ とクラスタ $i$ に所属している既存データから計算した $\boldsymbol{\mu}_c, \nu_c, S_q$ を使って $\boldsymbol{\theta}_i = (\boldsymbol{\mu}_i, \Lambda_i) = (\boldsymbol{\mu}_c, {\nu_c}S_q)$ とします。$s_k$ が新しいクラスタとなる場合は、$\boldsymbol{x}_k$ のみから計算した $\boldsymbol{\mu}_c, \nu_c, S_q$ を使って $\boldsymbol{\theta}_{new} = (\boldsymbol{\mu}_{new}, \Lambda_{new}) = (\boldsymbol{\mu}_c, {\nu_c}S_q)$ とします。$p(s_k=1|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x}),\,p(s_k=2|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x}),\, …,\, p(s_k=c|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x}),\, p(s_k=new|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x})$ の計算方法は以下の通りです。定数 $C$ が登場していますが、確率同士で比を取る時に消えます。
   $$p(s_k=i|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x}) = C\frac{n_i’}{n – 1 + \alpha}N(\boldsymbol{x}_k; \boldsymbol{\mu}_i’, \Lambda_i’)\,(i = 1, 2, …, c) \\
   p(s_k=new|\boldsymbol{\theta’}, \boldsymbol{s}_{-k}, \boldsymbol{x}) = C\frac{\alpha}{n – 1 + \alpha}(\frac{\beta}{(1 + \beta)\pi})^{d/2}\frac{|S_b|^{(\nu+1)/2}\Gamma(\frac{\nu+1}{2})}{|S|^{\nu/2}\Gamma(\frac{\nu + 1 – d}{2})}$$
   $n_i’$ は 1個抜き状態の時のクラスタ $i$ に所属するデータ数、$(\boldsymbol{\mu}_i’, \Lambda_i’)$ は同じく 1個抜き状態の時のクラスタ $i$ のパラメータの最尤推定値です。1個抜いた時、クラスタ $i$ から抜かれているか、それ以外から抜かれているか分かりませんが、抜かれているとも限らないので $’$ 付きで一時的に抜かれているかもしれない状況を表しています。また、$S_b$ は以下を満たします。
   $$S_b^{-1} = S^{-1} + \frac{\beta}{1 + \beta}(\boldsymbol{x}_k – \boldsymbol{\mu}_0)(\boldsymbol{x}_k – \boldsymbol{\mu}_0)^t$$
4. 1個抜いてまた戻したことにより、新しいクラスタ構成ができたので、クラスタの分割方法、配置について事後確率を計算します。$$\begin{align}p(\boldsymbol{\theta}, \boldsymbol{s}|\boldsymbol{x}) &∝ p(\boldsymbol{s})\prod_{i=1}^cG_0(\boldsymbol{\theta}_i)\prod_{i=1}^n p(\boldsymbol{x}_i|\boldsymbol{\theta}_{s_k}) \\
   &= \frac{\alpha^c\prod_{i=1}^c(n_i – 1)!}{AF(\alpha, n)}\prod_{i=1}^c\bigl[N(\boldsymbol{\mu}_i; \boldsymbol{\mu}_0, (\beta\Lambda_i)^{-1})W(\Lambda_i; \nu, S)\prod_{k \in cluster-i}N(\boldsymbol{x}_k; \boldsymbol{\mu}_i, \Lambda_i^{-1})\bigr]\end{align}$$
   $AF(\alpha, n)$ は上昇階乗であり、$(\boldsymbol{\mu}_i, \Lambda_i)$ はクラスタ $i$ のパラメータの最尤推定値です。コーディングの際には、上式そのままだと掛け算で精度が落ちてしまうかもしれないので、log を取って、掛け算の代わりに足し算にしてやるとよいと思います。
5. 1 – 3 を十分に繰り返して、3 で得られた事後確率が最大となる時が最適解とみなします。事後確率最大を与えた $\boldsymbol{\theta}, \boldsymbol{s} (= \boldsymbol{\theta}_1, \boldsymbol{\theta}_2, …, \boldsymbol{\theta}_c, s_1, s_2, …, s_n)$ が、最適なクラスタ分割、配置の答えとなります。

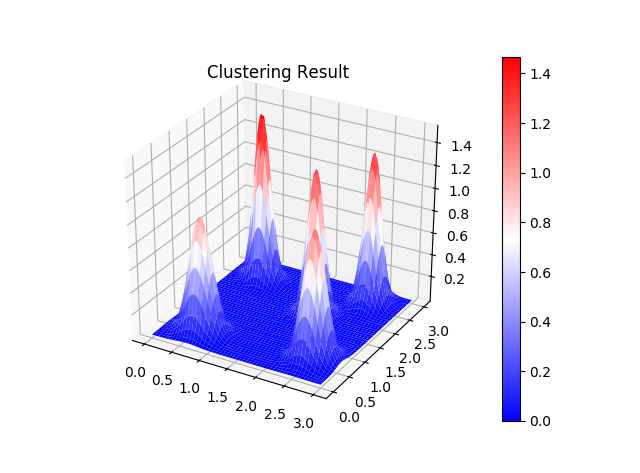
この手順を python で実装してみました。サンプルデータは一様乱数を使って適当に生成してみました。データは 3通り作ってみて、それぞれクラスタが 3個と判定してほしい、4個と判定してほしい、5個と判定してほしいというような恣意的なデータです。これらを試してみると、いい具合に期待通りに分割してくれました。
クラスタ3個への分割↓

クラスタ4個への分割↓

クラスタ5個への分割↓

ハイパーパラメータがいくつかあって、それを適切に設定してあげないといけないのですが、とりあえず以下のような値を選んでいます。
$$\alpha = 1.0,\,\beta = 0.3,\,S = \left(\begin{array}{rr}1 & 0 \\ 0 & 1\end{array}\right),\,\mu_0 = \frac{1}{n}\Sigma_{i=1}^n\boldsymbol{x}_i,\,\nu = 15$$
今回適当に作ったデータはきれいに分かれていて、クラスタリングするにはあまり間違いようがないので、適当なパラメータでもよかったのかもしれません。どのクラスタに所属させるか微妙な時とか、ハイパーパラメータによって結果が違ってくるのかもしれません。
せっかく実装したので、次回はもう少し色々試してみる予定です。

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。