ディリクレ過程混合モデルによるクラスタリングの直感的理解（後編）

前回の続きから

前回は、ディリクレ過程から生成されるであろうクラスタリングデータをベイズ推定するという方法で、クラスタリングデータを生成する方法について見てみました。この方法によって、クラスタ1 に $n_1$個、クラスタ2 に $n_2$個、・・・、クラスタc に $n_c$個のデータが所属するような c個のクラスタが生成されたとします。($n_1 + n_2 + … + n_c = n$)

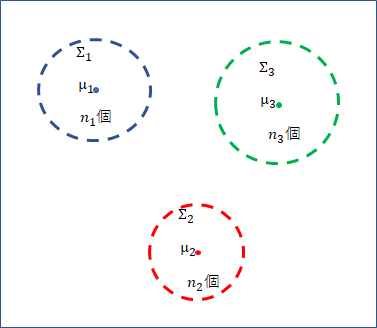
クラスタのパラメータは $\boldsymbol{\theta}_i (i = 1, 2, …, c)$ で表します。データが正規分布に従って生成されていると仮定する場合は、中心と分散をセットにした $\boldsymbol{\theta}_i = (\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i)$ のようなベクトルデータです。また、与えられたデータ $\boldsymbol{x}_i$ がどのクラスタに所属するかを表す変数として、$s_i$ を用意します。クラスタが $c$ 個だとすると、$s_i$ は $1, 2, …, c$ のどれかを保持します。
パラメータ $\boldsymbol{\theta}_i (i= 1, 2, …, c)$ を持ち、$n$ 個のデータが所属するクラスタ番号が $s_i$ で表されるとき、そのようなクラスタを生成する確率を $p(\boldsymbol{\theta}_1, \boldsymbol{\theta}_2, …, \boldsymbol{\theta}_c, s_1, s_2, …, s_n)$ と書くと、

$p(\boldsymbol{\theta}_1, \boldsymbol{\theta}_2, …, \boldsymbol{\theta}_c, s_1, s_2, …, s_n) = \frac{\alpha^c\prod_{i=1}^c(n_i – 1)!}{AF(\alpha, n)} G_0(\boldsymbol{\theta}_1) G_0(\boldsymbol{\theta}_2) … G_0(\boldsymbol{\theta}_c)$

となります。$\frac{\alpha^c\prod_{i=1}^c(n_i – 1)!}{AF(\alpha, n)}$ はイーウェンスの抽出公式と呼ばれる式であり、中華料理店過程 (CRP) の考え方から導かれます。$AF(\alpha, n)$ は $\alpha(\alpha + 1)(\alpha + 2)…(\alpha + n – 1)$ という上昇階乗 (Ascending Factorial) です。$\alpha$ は前回登場しましたが、ディリクレ過程さいころの目の出やすさを制御する集中度と呼ばれるパラメータです。
イーウェンスの抽出公式の部分は $n$ 個のデータを $n_1, n_2, …, n_c$ に分割する確率を表し、後半の $G_0(\boldsymbol{\theta}_1)G_0(\boldsymbol{\theta}_2) … G_0(\boldsymbol{\theta}_c)$ の部分はパラメータの値が $\boldsymbol{\theta}_i$ (i = 1, 2, .., c) となる確率を表します。$n_1, n_2, …, n_c$ 個に分割して、それぞれにパラメータ $\boldsymbol{\theta}_i$ を与えるという考え方に基づき、上式のように確率が計算されます。
ちなみに $G_0$ は、これも前回に登場したディリクレ過程さいころの基底分布であり、パラメータ $\boldsymbol{\theta}_i$ を生成するために使用されます。$G_0$ は確率密度関数である必要があります。

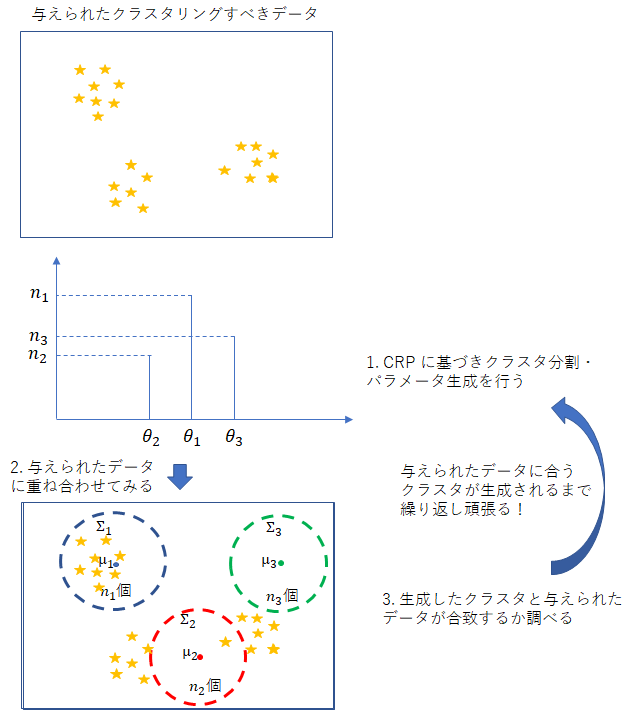
さて、今 $\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n$ がクラスタリングすべきデータとして与えられています。
仮に $c$ 個のクラスタに分割するとして、クラスタパラメータ $\boldsymbol{\theta}_1, \boldsymbol{\theta}_2, … , \boldsymbol{\theta}_c$ が与えられた時、$\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n$ が得られる確率を考えましょう。ただし、$\boldsymbol{\theta}_1$ には $n_1$ 個、$\boldsymbol{\theta}_2$ には $n_2$ 個、$\boldsymbol{\theta}_i$ には $n_i$ 個が所属するというような制約付きです。
$\boldsymbol{x}_i$ がどこのクラスタに所属するか、色々な組み合わせが考えられます。ここでは、色々な組み合わせのうち、一つの組み合わせについて考えてみます。まず $\boldsymbol{x}_1$ は $\boldsymbol{\theta}_1$ に所属するとしましょうか。$\boldsymbol{x}_1$ が $\boldsymbol{\theta}_1$ から生成される確率は、$p(\boldsymbol{x}_1|\boldsymbol{\theta}_1)$ となります。クラスタ分布が正規分布に従うなら、
$p(\boldsymbol{x}_1|\theta_1) = \frac{1}{2\pi^\frac{d}{2}|\boldsymbol{\Sigma_1}|^\frac{1}{2}}exp(-\frac{1}{2}(\boldsymbol{x_1} – \boldsymbol{\mu_1})^T\boldsymbol{\Sigma}_1^{-1}(\boldsymbol{x}_1 – \boldsymbol{\mu}_1))$
となります。$\boldsymbol{x}_1$ と $\boldsymbol{\mu}_1$ が近ければ確率は高くなりますが、遠いと低くなってしまいますね。確率が高いかどうかは分かりませんが、とにかく $\boldsymbol{x}_i$ が $\boldsymbol{\theta}_1$ に所属すると仮定した場合に生成される確率が分かりました。
$\boldsymbol{x}_1$ が $\boldsymbol{\theta}_1$ から生成される確率は得られたので、次 $\boldsymbol{x}_2$ に行ってみましょう。$\boldsymbol{x}_2$ はどこから生成しますかね。$\boldsymbol{\theta}_c$ から生成してみましょうか？生成確率は、$p(\boldsymbol{x}_2|\boldsymbol{\theta}_c)$ です。式の形はさっきと同じです。これで $\boldsymbol{x}_1$, $\boldsymbol{x}_2$ の2つの確率を計算できました。
今、$\boldsymbol{\theta}_1$ から 1個、$\boldsymbol{\theta}_c$ から 1個生成しましたが、残り $n-2$ 個あります。これらは、$\boldsymbol{\theta}_1$ には $n_1 – 1$個、$\boldsymbol{\theta}_2$ には $n_2$個、… $\boldsymbol{\theta}_c$ には $n_c – 1$ 個所属するように生成する必要があります。それを満たすように、とにかく頑張って $n$ 個生成したとしましょう。それらが生成される確率は、$p(\boldsymbol{x}_1|\boldsymbol{\theta}_1)p(\boldsymbol{x}_2|\boldsymbol{\theta}_c) …$ となります。これで一つの組み合わせの確率が得られました。

さて、なんでこのような確率を計算したかというと、以下のようなことをしたいからです。
今、何をやろうとしているかというと、与えられた $\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n$ をクラスタリングすることです。このためには、$\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n$ が与えられた時、$p(\boldsymbol{\theta}_1, \boldsymbol{\theta}_2, …, \boldsymbol{\theta}_c, s_1, s_2, …, s_n|\boldsymbol{x}_1, \boldsymbol{x}_2, … \boldsymbol{x}_n)$ を最大化するような $\theta_1, \theta_2, …, \theta_c, s_1, s_2, …, s_n$ が求められれば OK です。
このような $\theta_1, \theta_2, …, \theta_c, s_1, s_2, …, s_n$ が、$\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n$ が与えられた時、最も尤もらしいクラスタ分割・配置ということになります。即ち、クラスタは何個あって、そのクラスタのパラメータはそれぞれ $(\boldsymbol{\mu_j}, \boldsymbol{\Sigma_j})$ で、各 $\boldsymbol{x_i}$ はどのクラスタに所属して、ということが分かります。
なお、$p(\boldsymbol{\theta}_1, \boldsymbol{\theta}_2, …, \boldsymbol{\theta}_c, s_1, s_2, …, s_n|\boldsymbol{x}_1, \boldsymbol{x}_2, … \boldsymbol{x}_n)$ は書くのも読むのも大変なので、今後は $p(\boldsymbol{\theta}, \boldsymbol{s} | \boldsymbol{x})$ という表記にすることにします。
$p(\boldsymbol{\theta}, \boldsymbol{s} | \boldsymbol{x})$ のような添字なしの表記があったら、$p(\boldsymbol{\theta}_1, \boldsymbol{\theta}_2, …, \boldsymbol{\theta}_c, s_1, s_2, …, s_n|\boldsymbol{x}_1, \boldsymbol{x}_2, … \boldsymbol{x}_n)$ のような添字付きで読み替えてください。

ベイズの定理より、$p(\boldsymbol{\theta}, \boldsymbol{s}| \boldsymbol{x}) = p(\boldsymbol{\theta}, \boldsymbol{s})p(\boldsymbol{x}|\boldsymbol{\theta}, \boldsymbol{s}) / p(\boldsymbol{x}) ∝ p(\boldsymbol{\theta}, \boldsymbol{s})p(\boldsymbol{x}|\boldsymbol{\theta}, \boldsymbol{s})$ が成立します。最右辺第2項の部分が、先ほど考えた $p(\boldsymbol{x}_1|\boldsymbol{\theta}_1)p(\boldsymbol{x}_2|\boldsymbol{\theta}_c) …$ の部分になります。

1. クラスタが何個あって、各クラスタがどのようなパラメータを持って、というような分割・配置の方法を考え、そのような分割・配置を生成する確率を計算する ⇒ $p(\boldsymbol{\theta}, \boldsymbol{s})$
2. そのクラスタから $\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n$ を生成する確率を計算する⇒ $p(\boldsymbol{x}|\boldsymbol{\theta}, \boldsymbol{s})$
3. $p(\boldsymbol{\theta}, \boldsymbol{s}| \boldsymbol{x})
   ∝ p(\boldsymbol{\theta}, \boldsymbol{s})p(\boldsymbol{x}|\boldsymbol{\theta}, \boldsymbol{s})$ を計算し、これが最大となるようなクラスタの分割・配置、およびデータの配分方法を見つける

というわけで、$p(\boldsymbol{x}|\boldsymbol{\theta}, \boldsymbol{s})$ を計算する必要があって、具体例として一つ考えてみたのでした。

与えられた $\boldsymbol{x}$ の下で、$\boldsymbol{\theta}, \boldsymbol{s}$ を少しずつ動かしながら、$p(\boldsymbol{\theta}, \boldsymbol{s}| \boldsymbol{x})$ を最大化すればよいのですが、基本的には $\boldsymbol{\theta}, \boldsymbol{s}$ のすべての組み合わせを考えて、それぞれの組み合わせで $p(\boldsymbol{\theta}, \boldsymbol{s}| \boldsymbol{x}) ∝ p(\boldsymbol{\theta}, \boldsymbol{s})p(\boldsymbol{x}|\boldsymbol{\theta}, \boldsymbol{s})$ を計算し、その中の最大値を選ぶ必要があります。$p(\boldsymbol{\theta}, \boldsymbol{s})$ も $p(\boldsymbol{x}|\boldsymbol{\theta}, \boldsymbol{s})$ も計算できるのですが、組み合わせが大変なことになっているので、とても重い計算になります。
$\boldsymbol{s}$ の組み合わせからして何通りあるのでしょうか？ $_{n} C_{n_1}$ x $_{n-n_1} C_{n_2}$ x … x $_{n_c} C_{n_c}$ ですかね。
$\boldsymbol{\theta}$ に関しては、$\boldsymbol{\theta}$ が離散値ではないので、片っ端からすべて数え上げるという方法が使えません。やるとしたら、離散値扱いして近似することです。考えられるすべての組み合わせの中から最大値を選べばいいのですが、実際にはうまくいきません。

ギブスサンプリング

ここでギブスサンプリングが登場します。

ギブスサンプリングは、ある $n$ 個のデータが与えられている場合、そのデータが生成された確率分布から新しいデータを生成するサンプリング方法です。ただし、ギブスサンプリングを行うためには、条件付確率分布
$p(\boldsymbol{x}_i|\boldsymbol{x}_1, …, \boldsymbol{x}_{i-1}, \boldsymbol{x}_{i+1}, …, \boldsymbol{x}_n)$ の具体形が分かっていなければいけません。
ギブスサンプリングによって、都度 $(\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n)$ が生成されます。生成されたデータ $(\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n)$ は、ある確率分布 $p(\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n)$ に従います。その確率分布 $p(\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n)$ とは、条件付確率分布 $p(\boldsymbol{x}_i|\boldsymbol{x}_1, …, \boldsymbol{x}_{i-1}, \boldsymbol{x}_{i+1}, …, \boldsymbol{x}_n)$ を導くことができる元ネタの確率分布です。
$p(\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n)$ の具体形は分かっていないけど、$p(\boldsymbol{x}_i|\boldsymbol{x}_1, …, \boldsymbol{x}_{i-1}, \boldsymbol{x}_{i+1}, …, \boldsymbol{x}_n)$ の具体形は分かっているという状況で、未知の $p(\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n)$ に従う $(\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n)$ をサンプリングすることができるのがギブスサンプリングです。

1. $n$ 個のデータを適当に初期化する
2. $n$ 個のデータのうち、ランダムに一つを選択する ($\boldsymbol{x}_i$ とする)
3. $p(\boldsymbol{x}_i|\boldsymbol{x}_1, …, \boldsymbol{x}_{i-1}, \boldsymbol{x}_{i+1}, …, \boldsymbol{x}_n)$ という確率に従って、新しい値 $\boldsymbol{x}_i$ を生成する
4. 新しい $\boldsymbol{x}_i$ の値で古い $\boldsymbol{x}_i$ を置き換える
5. $(\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n)$ というサンプリングデータが得られる
6. 十分なサンプリングを行うまで 2 に返ってループする

という方法でサンプリングを行います。

今、我々が求めたいのは、$p(\boldsymbol{\theta}, \boldsymbol{s}|\boldsymbol{x})$ を最大にするような $\boldsymbol{\theta}, \boldsymbol{s} (= \boldsymbol{\theta}_1, \boldsymbol{\theta}_2, …, \boldsymbol{\theta}_c$ と $s_1, s_2, …, s_n)$ です。
この問題に対し、$p(s_i|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x})$ を使って確率的に $s_i$ を生成するギブスサンプリングを用いることにより、
$p(\boldsymbol{\theta}, \boldsymbol{s}|\boldsymbol{x})$ に従うサンプリングデータ　$\boldsymbol{\theta}, \boldsymbol{s}$ が得られます。ここで
$\boldsymbol{s}_{-1}$ は $(s_1, s_2, …, s_{i-1}, s_{i+1}, …, s_n)$ というような $\boldsymbol{s}$ 全体から $s_i$ だけを引いた集合の略記です。また、1個抜きの $s_1, s_2, …, s_{i-1}, s_{i+1}, …, s_n$ がクラスタ $\boldsymbol{\theta}_1, \boldsymbol{\theta}_2, …, \boldsymbol{\theta}_c$ に所属している状況において、各クラスタの所属数が $n_1´, n_2´, n_c´$ となります。$s_i$ 1個を抜いているので、元の $n_1, n_2, …, n_c$ のどれかから 1 減じられています。1 減じられた結果、所属数が 0 になり、消滅してしまうクラスタもあるかもしれません。その場合、クラスタ数は $c – 1$ となります。そのような「どれか1個抜けている」状況を $’$ 付きで表しています。

ここでは途中を省略しますが (省略しない場合はこちら)、$p(s_i|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x})$ は以下のように書くことができます。

$p(s_i|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}) ∝ p(s_i|\boldsymbol{s}_{-i}) p(x_i|\boldsymbol{\theta}_{s_i})$

右辺の計算は、$s_i$ が既存クラスタになるか、新規クラスタになるかによって変わります。

既存クラスタ $j$ の場合の右辺

• $p(s_i|\boldsymbol{s}_{-1}) = n_j’ / (n – 1 + \alpha)$
• $p(\boldsymbol{x}_i|\boldsymbol{\theta}_{s_i})$ は確率分布をあらかじめ適当に仮定しておき、それに従い計算します

新規クラスタの場合の右辺

• $p(s_i|\boldsymbol{s}_{-1}) = \alpha / (n – 1 + \alpha)$
• $p(\boldsymbol{x}_i|\boldsymbol{\theta}_{s_i}) = \int p(\boldsymbol{x}_i|\boldsymbol{\theta})G_0(\boldsymbol{\theta})d\boldsymbol{\theta}$
  $p(\boldsymbol{x}_i|\boldsymbol{\theta}_{s_i})$ は、新規クラスタがどのようなパラメータになるかは分からないため、期待値 $\int p(\boldsymbol{x}_i|\boldsymbol{\theta})G_0(\boldsymbol{\theta})d\boldsymbol{\theta}$ で代用するという考えに基づいています。

$p(s_i|\boldsymbol{s}_{-i})$ が上記のように

既存クラスタ j の場合は $n_j’ / (n – 1 + \alpha)$
新規クラスタの場合は $\alpha / (n – 1 + \alpha)$

と書ける理由を考えてみましょう。

前回の離散データ生成方法に基づき、データを作ることを考えます。今 $n-1$ 個目のデータまで作っていて、最後の $n$ 個目を生成するケースを考えてみましょう。これは、ギブスサンプリングでの 1個抜き状態から $s_i$ を生成する状況と似ています。
$n$ 個目のデータを既存のクラスタ $i$ に重ねる確率は $n_i / (n – 1 + \alpha)$, 新しく値を生成する確率は $\alpha / (n – 1 + \alpha)$ となるのでした。

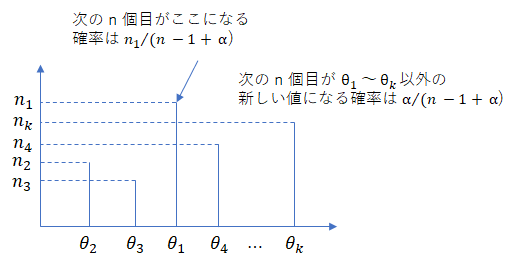
したがって、$p(s_n|\boldsymbol{s}_{-n})$ は、

既存クラスタ $j$ の場合
$p(s_n|\boldsymbol{s}_{-n}) = n_j’ / (n – 1 + \alpha) (j = 1, 2, …, c)$

新規クラスタの場合
$p(s_n|\boldsymbol{s}_{-n}) = \alpha / (n – 1 + \alpha)$

となります。
ただし、$p(s_n|\boldsymbol{s}_{-n})$ はギブスサンプリングで必要な式 $p(s_i|\boldsymbol{s}_{-1})$ と似ていますが、微妙に違います。$p(s_n|\boldsymbol{s}_-n)$ は最後のデータを生成する確率ですが、ギブスサンプリングで必要な式は、任意の $s_i$ の条件付き確率　$p(s_i|\boldsymbol{s}_{-i})$ なのでした。
しかし、CRP ではデータの生成順番を入れ替えても結果は同じになるので、

$p(s_i|\boldsymbol{s}_{-i}) = p(s_n|\boldsymbol{s}_{-n})$

が成立します。
というわけで、$p(s_i|\boldsymbol{s}_{-i})$ は、

既存クラスタ j の場合は $n_j’ / (n – 1 + \alpha)$
新規クラスタの場合は $\alpha / (n – 1 + \alpha)$

と書けることになります。

$p(s_i|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x})$ によってギブスサンプリングを行えば、$p(\boldsymbol{\theta}, \boldsymbol{s}|\boldsymbol{x})$ に従うサンプリングデータ
$\boldsymbol{\theta}, \boldsymbol{s}$ が得られるので、それらサンプリングデータの中から $p(\boldsymbol{\theta}, \boldsymbol{s}|\boldsymbol{x})$ の最大値を特定出来れば OK です。後は、最大値を特定する方法だけです。
途中省略しますが (省略しない場合はこちら)、

$p(\boldsymbol{\theta}, \boldsymbol{s}|\boldsymbol{x}) ∝ p(\boldsymbol{s})\prod_{i=1}^cG_0(\boldsymbol{\theta}_i)\prod_{i=1}^n p(\boldsymbol{x}_i|\boldsymbol{\theta}_{s_i})$

となります。ギブスサンプリングによってデータを生成するたびに、上式に従って　$p(\boldsymbol{\theta}, \boldsymbol{s}|\boldsymbol{x})$ を算出すればよいのです。右辺第1項はイーウェンスの抽出公式であり、問題なく算出することができます。第2項、第3項の算出も、$G_0$ および $p(\boldsymbol{x}_i|\boldsymbol{\theta}_i)$ の具体形が与えられていれば問題ありません。

これでようやくゴールです。

まとめ

もう少し詳細を加えて、ギブスサンプリングを使って最尤クラスタリングを求める方法をまとめます。

1. 与えられたデータ $\boldsymbol{x} (= \boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n)$ を適当なクラスタに分割して $\boldsymbol{\theta} (= \boldsymbol{\theta}_1, \boldsymbol{\theta}_2, …, \boldsymbol{\theta}_c), \boldsymbol{s} (= s_1, s_2, …, s_n)$ の初期値を決めます。それぞれ別々の $n$ 個のクラスタに所属すると考えても OK です。その場合は、$s_i$ の初期値は $s_1 = 1, s_2 = 2, … s_n = n$ というようになり、クラスタ数 $c$ は $n$ になります。$\boldsymbol{\theta}_i$ に関しては、各クラスタから正規分布に従うデータが生成されると仮定する場合は、初期値は $\boldsymbol{\theta}_i = (\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i) = $(<最尤推定平均>, <最尤推定共分散>) となるようにします。
2. $s_i$ のいずれかをランダムに抜きます。その上で、$p(s_i|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}) ∝ p(\boldsymbol{x}_i|\boldsymbol{\theta}_{s_i}) p(s_i|\boldsymbol{s}_{-i})$に基づき、$s_i$ を確率的に生成します。確率的に生成するとは、$p(s_i=1|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}), p(s_i=2|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}), …, p(s_i=c|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}), p(s_i=new|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x})$ がそれぞれ計算できるので、例えば 0 – 1 の一様乱数を生成して、得られた値 $r$ が $0 \leq r < p(s_i=1|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x})$ ならば $s_i = 1$ とし、$p(s_i=1|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}) \leq r < p(s_i=1|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}) + p(s_i=2|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x})$ ならば $s_i = 2$, … とすれば OK です。$s_i$ が既存クラスタ $j$ に所属することになれば、$\boldsymbol{x}_i$ とクラスタ $j$ に所属している既存データから平均、分散を最尤推定して $\boldsymbol{\theta}_j$ とします。$s_i$ が新しいクラスタとなるならば、$\boldsymbol{\theta}_i = (\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i) = $(<最尤推定平均>, <最尤推定共分散>) とします。
3. $p(\boldsymbol{\theta}, \boldsymbol{s}|\boldsymbol{x}) ∝ p(\boldsymbol{s})\prod_i^cG_0(\boldsymbol{\theta}_i)\prod_{i=1}^n p(\boldsymbol{x}_i|\boldsymbol{\theta}_{s_i})$に基づき、クラスタの分割方法、配置について、確率を計算します。
4. 1 – 3 を十分に繰り返して、3 で得られた確率が最大となる時が最適解とみなします。確率最大を与えた $\boldsymbol{\theta}, \boldsymbol{s} (= \boldsymbol{\theta}_1, \boldsymbol{\theta}_2, …, \boldsymbol{\theta}_c, s_1, s_2, …, s_n)$ が、クラスタ分割、配置の答えとなります。

直感的と謳いつつ、割と理屈詰めの記事になってしまいました。
ギブスサンプリングは、

・$p(\boldsymbol{x}_i|\boldsymbol{x}_{-i})$ により $\boldsymbol{x}_i$ を確率的に生成する
・そうすると、$p(\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n)$ に従うデータ $\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n$ が得られる

という方法です。
「与えられたデータに対して、それを尤もらしく説明するクラスタ分割・配置を得る」という課題において、ギブスサンプリングを用いることにより、膨大な計算を回避することができます。

ディリクレ過程によるクラスタリング方法は、

a. クラスタ分割する方法をディリクレ分布をベースに尤もらしい方法で生成する
b. 与えられたデータに尤も適合するクラスタ分割を探す計算をギブスサンプリングにより軽減する

という巧みな方法です。
単に式を追うだけだと分かったような分からなかったような状態になりがちです。上記 a, b を意識しながら理解してみてください。

今回と前回の記事の内容を簡単に絵にしてみました。

補足

途中を省略してしまった箇所を補っておきます。

$p(s_i|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}) \\
= p(s_i|\boldsymbol{x}_i, \boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}_{-i}) [ただの書き換え] \\
= p(s_i, \boldsymbol{x}_i|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}_{-i}) / p(\boldsymbol{x}_i|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}_{-i}) \\
∝ p(s_i, \boldsymbol{x}_i|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}_{-i}) [s_i 間での比率を取るので、s_i で共通の分母は不要] \\
= p(\boldsymbol{x}_i|s_i, \boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}_{-i}) p(s_i|\boldsymbol{\theta’}, \boldsymbol{s}_{-i}, \boldsymbol{x}_{-i}) \\
= p(\boldsymbol{x}_i|\boldsymbol{\theta}_{s_i}) p(s_i|\boldsymbol{s}_{-i}) [x_i の所属クラスタのパラメータだけ分かれば x_i は生成できる、\\ ディリクレ過程混合モデルなので CRP が適用出来るので \boldsymbol{s}_{-1} だけ分かれば s_i は生成できる]$

$p(\boldsymbol{\theta}, \boldsymbol{s}|\boldsymbol{x}) \\
= p(\boldsymbol{\theta}, \boldsymbol{s}) p(\boldsymbol{x}|\boldsymbol{\theta}, \boldsymbol{s}) / p(\boldsymbol{x}) \\
= p(\boldsymbol{\theta})p(\boldsymbol{s}) p(\boldsymbol{x}|\boldsymbol{\theta}, \boldsymbol{s}) / p(\boldsymbol{x}) \\
∝ p(\boldsymbol{\theta})p(\boldsymbol{s}) p(\boldsymbol{x}|\boldsymbol{\theta}, \boldsymbol{s}) [サンプリングデータ間で分母は共通なので不要] \\
= p(\boldsymbol{s})\prod_{i=1}^cG_0(\boldsymbol{\theta}_i)\prod_{i=1}^n p(\boldsymbol{x}_i|\boldsymbol{\theta}_{s_i}) [各クラスタの生成確率と各データの配置確率] $

修正

• 正規分布のパラメータを $(\boldsymbol{\nu}, \boldsymbol{\Lambda})$ と記載していましたが、一般的な表記 $(\boldsymbol{\mu}, \boldsymbol{\Sigma})$ に直しました。
• 最初と最後の図にも $(\boldsymbol{\nu}, \boldsymbol{\Lambda})$ と記載してしまっていたため、修正して図を差し替えました。
• 正規分布の数式が誤っていたため、修正しました。
• ギブスサンプリングの手順にて、クラス選択の際の添え字、事後確率の式が誤っていたので修正しました。
• ギブスサンプリングの手順にて、クラスタのパラメータ推定を $(\boldsymbol{x}_i, 0)$ 等としていましたが、(<最尤推定平均>, <最尤推定共分散>) と書き改めました。<最尤推定平均>, <最尤推定共分散>
  については簡単に書けないので、次回に詳細を書きます。

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。