ディリクレ過程混合モデルによるクラスタリングの直感的理解（前編）

特徴空間上に分布した $n$個のパターン $x_1, x_2, …, x_n$ を、いくつかの塊に分割することを考えます。いくつの塊 (クラスタ) に分割すべきなのか？は分かっていません。このような状況でパターンを適切にクラスタに分割する方法、即ちクラスタリングについて考えます。

ここでは、ディリクレ過程混合モデルによるクラスタリングについて考えてみます。ディリクレ過程混合モデルによるクラスタリングは、事前にクラスタがいくつあるか知らなくても、適切に分割できる優れた方法です。k-means 法などでは、あらかじめクラスタがいくつなのか、指定する必要があります。ただ、ディリクレ過程混合モデルによるクラスタリングは、全体像を捉えるのが難しいです。そこで、この記事では細部を適当に省略しつつ、直感的に理解することを目指します。

ディリクレ過程混合モデルとは

ディリクレ過程混合モデルはノンパラメトリックベイズモデルの一つであり、ベイズモデルという名前がつくように、事後確率を最大化するような分割方法を探す方法です。基本的な考え方は、以下のようにシンプルなものです。

1. 何らかの方法によって離散分布を生成する
2. 離散分布から $n$個のデータを生成し、クラスタを形成する
3. そのクラスタから、与えられた観測パターンが生成される確率を計算する
4. ありとあらゆる離散分布を考えて、上記方法によりそれぞれの離散分布から観測パターンが得られる確率を計算する
5. これらの中で、最も確率が高い離散分布が、最も尤もらしいクラスタリングであると考える

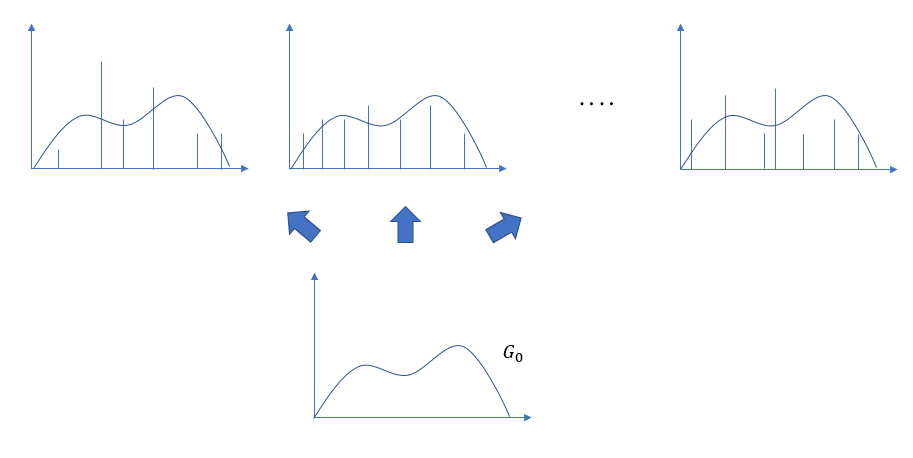
このステップ 1, 2 で登場するのがディリクレ過程です。ディリクレ過程は、任意の離散分布を生成しうる確率過程です。ディリクレ過程のイメージはさいころであって、ディリクレ過程さいころを振ると、その目に応じた離散分布を生成するようなものです。出せる目の数は無限大で、どのような離散分布でも生成できます。ただし、どの目も等確率で出るわけではありません。ディリクレ過程さいころの出る目を制御するのは、基底 $G_0$ と集中度と呼ばれるパラメータ $α$ です。

ディリクレ過程ではどのような目が出やすいのでしょうか。出る目の傾向は、どのようになっているのでしょうか？

• ディリクレ過程というさいころを1回振ると、出た目に従ってある離散分布 $G$ が生成されます
• ディリクレ過程さいころは無限の目を持ち、無数の離散分布を生成することができます
• 生成される離散分布は確率分布なので、足し合わせると 1 になります
• 生成される離散分布 $G$ の形状は分かりません
• ただし、以下のことは分かっています
  • $G$ から生成された離散データは、その形状は $G_0$ に近くなる
  • $α$ の値によって、$G$ から生成された離散データのばらけ度合いが変わる

困ったことに、さいころを 1回振るごとに出てくるはずの離散分布 $G$ の形状が分かりません。離散分布からデータを作りたいと思っていたのですが、できません。ディリクレ過程が離散分布を生成してくれて、与えられた分布から離散データ（＝クラスタ）を生成する流れだと思ったのに・・・。分かっているのは、生成される離散データの傾向だけです。

仕方がないので、離散分布から生成されうるデータを生成してみましょう。離散分布を生成して、そこから離散データを生成して、という2段階ではなくて、一気に離散データを作ってしまうのです。幸い、ディリクレ過程さいころが生成した離散分布から生成される離散データの傾向は分かっているので、それに合わせて作りましょう。

生成するデータは、$θ_1$ が $n_1$個、$θ_2$ が $n_2$個、… $θ_k$ が $n_k$個といったような離散データです。

まず 1個目のデータを生成しましょう。
ディリクレ過程から生成された離散データは基底 $G_0$ に従うので、我々が生成する離散データも $G_0$ 分布に従うものとしましょう。1個目は $G_0$ から生成しましょう。

$G_0$ から生成した結果、1個目として $θ_1$ が得られたとします。$θ_1$ は、１つ目のクラスタになります。

2個目のデータを生成しましょう。
2個目は $θ_1$ と同じ値でもよいですし、それ以外の新しい値でもよいです。それ以外の新しい値の場合は、1個目の場合と同じように $G_0$ から生成しましょう。でないと、長い目で見た場合にデータが $G_0$ に近くならないです。$θ_1$ と同じ値を生成する場合は、$θ_1$ のところに積み重ねましょう。この場合の離散データは、$θ_1$ が 2個となっているような形状となっています。

それ以外の $θ_2$ を生成する場合は、$θ_2$ のところに1個置きましょう。この場合の離散データは、$θ_1$ が 1個、$θ_2$ も 1個となっているような形状となっています。

では、$θ_1$ を生成する確率と、それ以外の新しい値を生成する確率は、どう配分するのがよいでしょうか？

ここで $α$ が出てきます。$α$ は、基底 $G_0$ から生成するか、既存クラスタから生成するかを決める重みづけです。既存クラスタが 1つの場合は、$\frac{α}{α+1} : \frac{1}{α+1}$ で重みづけします。つまり、$θ_1$を生成する確率は $\frac{1}{α+1}$, それ以外の新しい値を生成する確率は $\frac{α}{α+1}$ とします。新しい値を生成する場合は、繰り返しになりますが、$G_0$ に従ってデータを生成します。

次に 3個目です。
$θ_1$ のみにデータがある場合は、$θ_1$ に重ねてもよし、他の新しい値を生成するもよしです。$θ_1$, $θ_2$ にデータがある場合は、$θ_1$, $θ_2$に重ねてもよし、他の新しい値を生成するもよしです。

新しい値を生成する場合は、今までと同じように $G_0$ に従ってデータを生成します。この場合、$θ_1$ もしくは $θ_2$ のクラスタに重ねる確率と、新しく値を生成する確率は、$\frac{1}{α+2} : \frac{1}{α+2}$ : $\frac{α}{α+2}$ とします。生成した値は、$θ_1$ もしくは $θ_2$ に重ねるか、$θ_3$ のところに新しく1個置きましょう。

このような感じで 4個目、… n個目とデータを生成し、離散データを作っていきます。

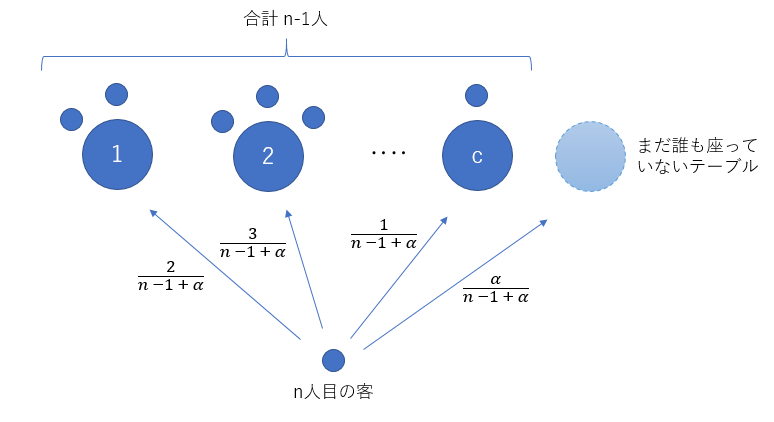
すでに c個のクラスタがあり、それぞれ $n_1個、n_2個、…, n_c$個、合計 $m$ 個のデータを積み重ねているとすると、既存のクラスタに重ねる確率と、新しく値を生成する確率は、$\frac{n_1}{α+m} : \frac{n_2}{α+m} : … : \frac{n_c}{α+m} : \frac{α}{α+m}$ とします。新しい値を生成する場合は、今までと同じように $G_0$ に従ってデータを生成します。

こうして得られた離散データは、かなりそれっぽい離散データになっているのではないでしょうか？
$G_0$ っぽくなっているはずですし、$α$ の値によってクラスタのばらけ度合いが変動するのも実現できていそうです。

本当にそれっぽいかどうか、怪しいのは $\frac{n_1}{α+m} : \frac{n_2}{α+m} : … : \frac{n_c}{α+m} : \frac{α}{α+m}$  で重みづけしているところですかね。何となく良さそうにも思えますが、確率的にどうなのか・・・。

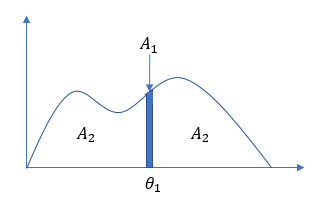
実はこの部分は、ディリクレ分布の事後分布の考え方を使っていて、ベイズ推定による最良の選択を行っているのです。例えば、1個目に $θ_1$ を生成した後、2個目を生成する時のことを考えます。$θ_1$ が立った個所の微小領域を $A_1$, それ以外の領域を $A_2$ というように2つの領域に分割します。

次のデータを $A_1$ から生成するか、$A_2$ から生成するかはディリクレ分布に従って決めます。$A_1$ から生成するということは、次のデータが $θ_1$ となることを、$A_2$ から生成するということは次のデータが $θ_1$ 以外の新しい離散値となることを意味します。$A_1$ から出やすいか、$A_2$ から出やすいかというパラメータは、ディリクレ分布に従わせます。

何故ディリクレ分布を持ち出すかというと、多項分布のパラメータを推定する際に出てくるのがディリクレ分布だからです。今、「既出の $θ_1$」「$θ_1$以 外の新しい値」という二項のみを取りうる二項分布を考えています。（話の都合上、多項分布が二項分布になってしまっていますが。）どれが出やすいかを推定してくれるのがディリクレ分布なのです。

ディリクレ分布の関数は以下のような引数を取るものにします。

$Dir(αG_0(A_1)+1+1, αG_0(A_2)+1) ≒ Dir(2, α+1)$

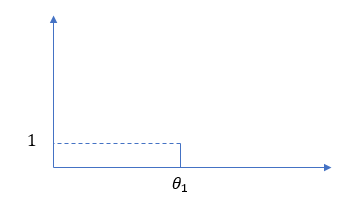
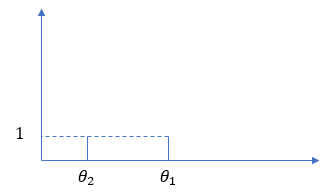
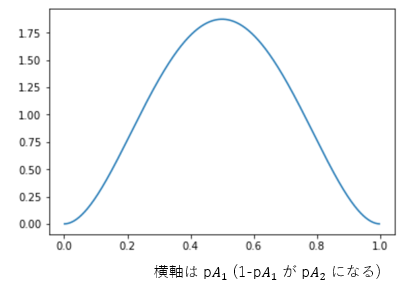
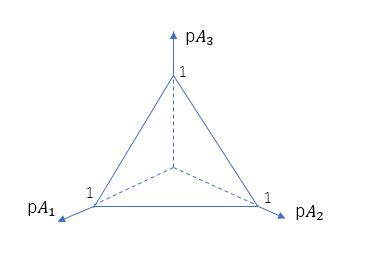
($G_0(A_1)$, $G_0(A_2)$ というのは領域 $A_1$, 領域 $A_2$ の面積です。 $G_0(A_1)$ は微小領域なので、0 とみなせます。$G_0(A_2)$ はほぼ $G_0$ 全体ですので、1 とみなせます。)ここで、第1引数に対応する第1のパラメータは $A_1$ からデータが出る確率 $pA_1$、第2引数に対応する第2のパラメータは $A_2$ から出る確率 $pA_2$ を表します。図にするとこんな感じです。($α=2$ の場合です)

$Dir(2, α+1)$ の頂点は、$pA_1$ が $\frac{1}{α+1}$, $pA_2$ が $\frac{α}{α+1}$ のところにあります。つまり、$A_1$ の出やすさと $A_2$ の出やすさは $\frac{1}{α+1}:\frac{α}{α+1}$ とするのが最も尤もらしいということになります。なので、$θ_1$ を生成する確率は $\frac{1}{α+1}$, それ以外の新しい値を生成する確率は $\frac{α}{α+1}$ としたのは正しい戦略だったのです。

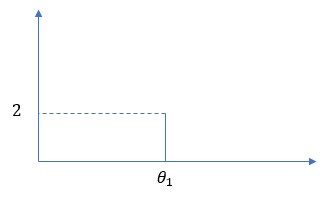
また、ディリクレ分布は、多項分布に従うデータを反映させると、またディリクレ分布になるという事実も重要です。データを反映させると反映されたデータが出やすくなるように確率分布を変えます。たとえば、$θ_1$ が 2回連続で出たとします。この結果を見たら、$θ_1$ って出やすいんじゃない？って思えるので、$θ_1$ の出る確率は上がるべきです。実際、これを反映させたディリクレ分布は $Dir(3, α+1)$ となり、$pA_1$ が $\frac{2}{α+2}$, $pA_2$ が $\frac{α}{α+2}$ のところに頂点が移動して、$A_1$ からの出やすさがアップします。
次に生成するデータは、$pA_1$:$pA_2$ = $\frac{2}{α+2}:\frac{α}{α+2}$ の確率で生成するのが合理的ということになります。これを表しているのが下の図です。先ほどと同じく $α=2$ の場合の図ですが、頂点が右に移動して、$A_1$ が出やすくなっています。

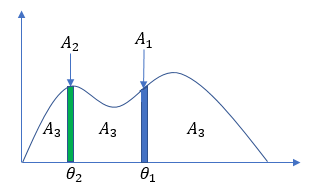
同じように、$θ_1$ と $θ_2$ が立っている時に 3個目のデータを生成させるケースを考えます。$θ_1$ が立った個所の微小領域を $A_1$, $θ_2$ が立った個所の微小領域を $A_2$, それ以外の領域を $A_3$ として分割します。

次のデータを $A_1$, $A_2$, $A_3$ のどれから生成するかはディリクレ分布に従って決めます。$A_1$ から生成するということは、次のデータが $θ_1$ となることを、$A_2$ から生成するということは次のデータが $θ_2$ となることを、$A_3$ から生成するということは次のデータが $θ_1$, $θ_2$ 以外の新しい離散値となることを意味します。$A_1$ から出やすいか、$A_2$ から出やすいか、はたまた $A_3$ から出やすいかというパラメータは、ディリクレ分布に従わせます。

ディリクレ分布の関数は以下のような引数を取るものにします。

$Dir(αG_0(A_1)+1+1, αG_0(A_2)+1+1, αG_0(A_3)+1) ≒ Dir(2, 2, α+1)$

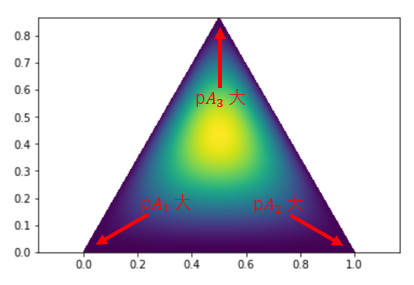
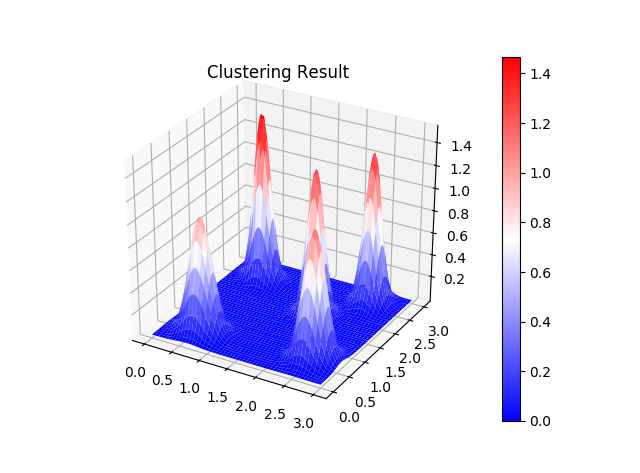
第1引数に対応する第1のパラメータは $A_1$ からデータが出る確率 $pA_1$、第2引数に対応する第2のパラメータは $A_2$ から出る確率 $pA_2$、第3引数に対応する第3のパラメータは $A_3$ から出る確率 $pA_3$ を表します。3次元の場合の分布はちょっと分かりにくいですが、正三角形は $pA_1 + pA_2 + pA_3 = 1$ を満たす平面を垂直方向から見ていると思ってください。色の濃淡が等高線を表していて、温度が高そうなところが確率が高いことを表しています。

$Dir(2, 2, α+1)$ の頂点は、$pA_1$, $pA_2$ が $\frac{1}{α+2}$, $pA_3$ が $\frac{α}{α+2}$ のところにあります。つまり、$pA_1$, $pA_2$, $pA_3$ の比率は $\frac{1}{α+2}:\frac{1}{α+2}:\frac{α}{α+2}$ とするのが最も尤もらしいということになります。なので、$θ_1$ もしくは $θ_2$ を生成する確率は $\frac{1}{α+2}$, それ以外の新しい値を生成する確率は $\frac{α}{α+2}$ とすればよいのです。パラメータが3個までのディリクレ分布なら図にして可視化することができますが、4個以上だとできません。ですが、考え方は同じです。

このように、生成されたデータを反映させつつディリクレ分布的に最も確率の高いところを狙って離散データを生成していくと、最も尤もらしくなることになります。つまり、ディリクレ分布の事後分布に基づきながら離散データの生成を行っていることになるので、最終的に得られた離散データは、最も出やすい離散データを生成しやすい、尤もらしい分布になっているのです。ディリクレ過程から生成された離散分布から生成された離散データを、ベイズ推定していると言えます。

この離散データの生成方法は、中華料理店過程 (Chinese Restaurant Process = CRP) と全く同じ式です。

CRP によって生成された分割方法は、ディリクレ過程から生成された離散分布から生成された離散データを、ベイズ推定しているのです。ディリクレ過程から生成される離散分布は分からなくても、その離散分布から生成された離散データを CRP はベイズ推定してくれるのです。CRP を使ってクラスタ生成をするのが合理的となると、イーウェンスの抽出公式が使えて便利です。n個のデータから c個のクラスタ $θ_1$, $θ_2$, … $θ_c$ を生成する尤度は以下のようになるでしょう。

$p(θ)$ = (イーウェンスの抽出公式) x $G_0(θ_1)$ x $G_0(θ_2)$ x … x $G_0(θ_c)$

この式は、ギブスサンプリングを行う際、事後確率最大を調べるのに使用します。これまでのところで、尤もらしい離散データを自由に生成できるようになりました。この後は、観測データに最もフィットするクラスタリングはどれかを探す作業になります。$p(θ|x) ∝ p(θ)p(x|θ)$ を最大化するような $θ$ を求めればよいのです。$p(θ)$ は、あらゆる$θ$について求めることができるようになりました。$p(x|θ)$ も、頑張れば計算できます。あらゆる $θ$ に対して $p(θ)p(x|θ)$ を計算して、最大となる $θ$ を探し出せば OK です。

ですが、これは組み合わせが多すぎて計算量が爆発してしまいます。

とても解けません。これを解決するのがギブスサンプリングです。

(次回に続く)

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。